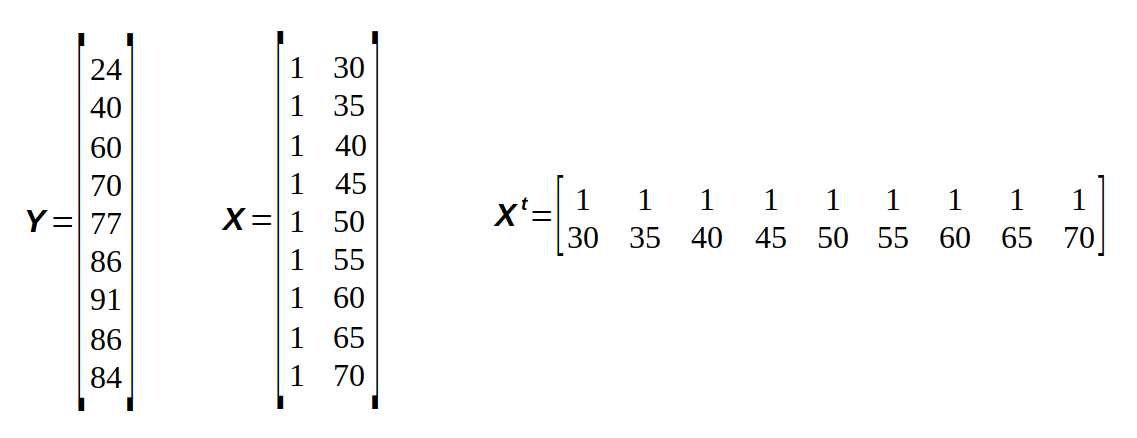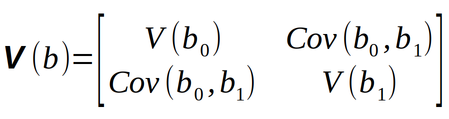Mas o que é um Modelo?
Resumidamente, um Modelo pode ser entendido como “Uma tentativa de representação simplificada e aproximada de uma realidade”! (Fonte: www.waterontheweb.org)
Todo trabalho de pesquisa visa o desenvolvimento de um Modelo que descreva o comportamento de um sistema a partir de um conjunto de informações mensuráveis. Um Modelo é uma “ferramenta” para fazer simulações e consequentemente previsões de cenários futuros.
Para mais informações sobre a importância dos modelos para o tema Água veja a seção E o Meio Ambiente?.
Nessa seção vamos mostrar a aplicação prática da técnica de Análise de Regressão Univariada no desenvolvimento de Modelos Empíricos a partir de dados experimentais.
Neste caso o objetivo é encontrar uma equação matemática que permita estabelecer a relação entre uma variável “independente” (usualmente reprensentada por x) com uma variável “dependente” (usualmente representada por y).
E vamos usar a linguagem Python para ilustrar alguns exemplos de cálculos estatísticos usando Matrizes.
Considere o experimento no qual uma reação foi feita em 9 diferentes temperaturas conforme a tabela da figura S.1.
Tabela S.1. Variação do rendimento da reação em função da temperatura, na faixa de 30-70°C. (Fonte: Como fazer experimentos, 2001)
| Temperatura (°C) | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 |
| Rendimento (%) | 24 | 40 | 60 | 70 | 77 | 86 | 91 | 86 | 84 |
Vamos representar o modelo que descreve a variação do rendimento com a temperatura através da equação S.1
Equação S.1. Modelo empírico linear para descrever a variação do rendimento da reação com a temperatura.
yi = β0 + β1×ti + εi
Onde yi é o rendimento correspondente à temperatura ti, εi é o erro aleatório associado à determinação do rendimento e os termos β0 e β1 são chamados de “parâmetros do modelo”.
Para determinar os parâmetros β0 e β1 da equação S.1 deve-se “ajustar” a equação S.1 aos 9 pares de valores (yi, ti) = (rendimento, temperatura) da tabela S.1, ou seja, resolver um sistema de 9 equações:
y1 = β0 + β1×t1 + ε1
y2 = β0 + β1×t2 + ε2
y3 = β0 + β1×t3 + ε3
.................................
y9 = β0 + β1×t9 + ε9
Esse sistema de equações pode ser representado de maneira mais compacta na forma de uma “equação matricial” como mostra a figura S.1.
Figura S.1. Equação matricial representando o sistema de 9 equações do modelo empírico “linear” que descreve a relação rendimento e temperatura descrita na tabela S.1 (Fonte: Como fazer experimentos, 2001)
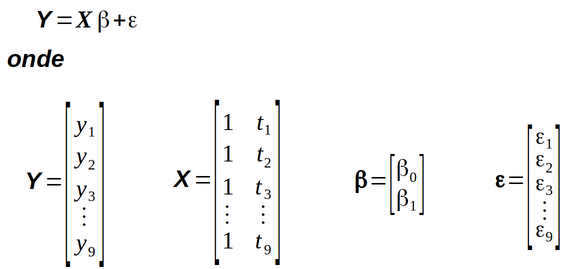
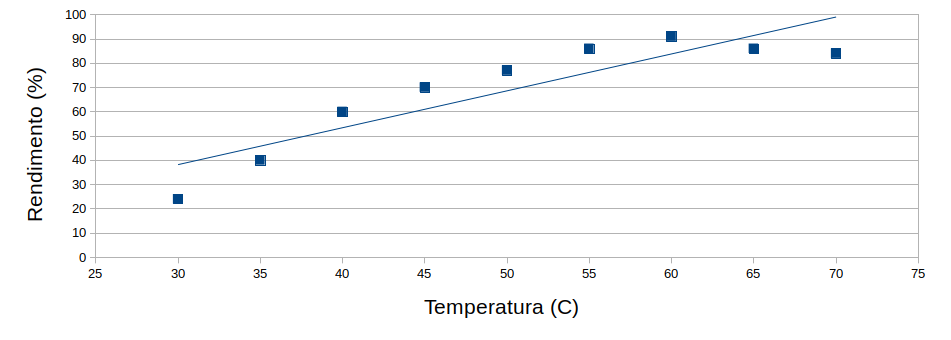
Como se pode observar pela figura S.2, não e possivel traçar uma reta que passe por todos os pontos experimentais.
Figura S.2. Gráfico com os resultados experimentais da tabela S.1 e uma reta de regressão.(Gráfico feito com o programa Calc)
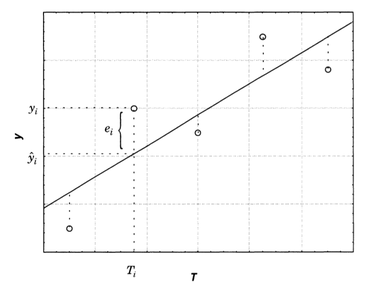
As diferenças entre os rendimentos experimentais (yi) e os rendimentos previstos pela reta de regressão (ŷi) são os chamados “resíduos” (ei). (Figura: S.3)
Se na temperatura ti o rendimento observado é yi e o rendimento previsto pela reta de regressão é ŷi, dizemos que o resíduo deixado pelo modelo é:
ei = yi − ŷi
onde ŷi = b0 + b1ti, sendo b0 e b1 os coeficientes que definem o intercepto e a inclinação da reta, respectivamente. Ou seja, são “estimativas” de β0 e β1, respectivamente.
E a melhor reta será aquela que passar “mais perto” dos pontos experimentais, minimizando os resíduos.
Como os valores de yi já são conhecidos de antemão, os resíduos irão depender apenas dos valores calculados de b0 e b1 . No ajuste por “mínimos quadrados”, esses valores são aqueles que tornam o somatório Σei2 o menor possível.
Podemos calcular os valores de b0 e b1 diretamente pela equação matricial S.2.
Equação S.2. Equação matricial geral para o ajuste de modelos pela técnica dos “mínimos quadrados”.
b = (XtX)-1 XtY
Essa é uma equação importante pois é uma solução geral para o ajuste de um modelo por mínimos quadrados quando o número de observações (dados experimentais) é maior do número de parâmetros do modelo.
A matriz “X” é construída preenchendo-se a primeira coluna com o número “1” e colocando na segunda coluna as variáveis experimentais, neste caso, temperaturas. E “Xt” representa a “transposta” da matriz “X”, como mostra a figura S.4.
A matriz “Y” é a matriz dos “resultados experimentais”, ou seja, os valores da função para as diferentes condições experimentais, neste caso, rendimento.
O termo “XtX” representa o produto matricial entre “Xt” e “X”.
Nota
O produto de matrizes NÃO é uma operação “comutativa”, e portanto (XtX) é ≠ de (XXt)
Com os dados da tabela S.1 podemos montar as matrizes da figura S.4
As manipulação de matrizes no Python são feitas comumente com o uso da biblioteca NumPy.
Vamos criar um script em Python com o cabeçalho:
#!/usr/bin/env python3 # -*- coding: utf8 -*-
E “carregar” a biblioteca NumPy com o comando import numpy as np.
Nota
Vamos utilizar o interpretador do Python 3.5.3 no modo interativo no terminal para ilustrar as etapas de cálculo.
A matriz “Y” pode ser criada de duas formas:
>>> Y_exp = np.array([[24], [40], [60], [70], [77], [86], [91], [86], [84]])
>>> Y_exp
array([[24],
[40],
[60],
[70],
[77],
[86],
[91],
[86],
[84]])
Mas também pode ser criada como uma lista (1 dimensão) e posteriormente transformada em uma matriz (2 dimensões) com o comando:
>>> Y = np.array([24, 40, 60, 70, 77, 86, 91, 86, 84])
>>> Y.shape
(9,)
>>> Y_exp = Y_exp.reshape(-1,1)
>>> Y_exp
array([[24],
[40],
[60],
[70],
[77],
[86],
[91],
[86],
[84]])
>>> Y_exp.shape
(9, 1)
Um exemplo de matriz de dados “X” pode ser criada com os comandos:
>>> X = np.array([[1, 30], [1, 35], [1, 40], [1, 45], [1, 50], [1, 55], [1, 60], [1, 65], [1, 70]])
>>> X
array([[ 1, 30],
[ 1, 35],
[ 1, 40],
[ 1, 45],
[ 1, 50],
[ 1, 55],
[ 1, 60],
[ 1, 65],
[ 1, 70]])
Mas também pode ser “montada” com o comando:
X = np.array([[30, 35, 40, 45, 50, 55, 60, 65, 70]])
>>> X
array([[30, 35, 40, 45, 50, 55, 60, 65, 70]])
>>> X = X.T
>>> X
array([[30],
[35],
[40],
[45],
[50],
[55],
[60],
[65],
[70]])
>>> X = np.hstack([np.ones(X.shape), X])
>>> X
array([[ 1., 30.],
[ 1., 35.],
[ 1., 40.],
[ 1., 45.],
[ 1., 50.],
[ 1., 55.],
[ 1., 60.],
[ 1., 65.],
[ 1., 70.]])
E a sua transposta “X_t”:
>>> X_t = X.T
>>> X_t
array([[ 1, 1, 1, 1, 1, 1, 1, 1, 1],
[30, 35, 40, 45, 50, 55, 60, 65, 70]])
O produto matricial “XtX” (X_t_prod_matricial_X) é obtido pelo comando:
>>> X_t_prod_matricial_X = np.dot(X_t,X)
>>> X_t_prod_matricial_X
array([[ 9, 450],
[ 450, 24000]])
E a matriz inversa do produto de Xt por X é:
>>> inv_X_t_dot_X = np.linalg.inv(X_t_prod_matricial_X)
>>> inv_X_t_dot_X
array([[ 1.77777778e+00, -3.33333333e-02],
[-3.33333333e-02, 6.66666667e-04]])
O segundo termo da equação S.2 ((XtY) pode ser calculado pelo comando:
>>> X_t_Y_exp = np.dot(X_t,Y_exp) >>> X_t_Y_exp array([ 618, 33180]) >>> X_t_Y_exp.shape (2,)
Podemos observar que o resultado do produto matricial de Xt por Y é uma estrutura no formato de lista (unidimensinal). Para transformar em uma matriz de 2 linhas por 1 coluna, usamos o “método” reshape.
>>> X_t_Y_exp = X_t_Y_exp.reshape(-1,1)
array([[ 618],
[33180]])
>>> X_t_Y_exp.shape
(2, 1)
E finalmente a matriz “B” com os parâmetros da equação de regressão é calculada com o comando:
>>> B = np.dot(inv_X_t_dot_X, X_t_Y_exp)
>>> B
array([[-7.33333333],
[ 1.52 ]])
>>> B.shape
(2, 1)
Portanto, de acordo com a equação S.2, as etapas para o cálculo da matriz de parâmetros “b” é representada na figura S.5
Figura S.5. Etapas para o cálculo matricial dos parâmetros do modelo (b0 e b1) aplicando as matrizes da figura S.4 na equação S.2.
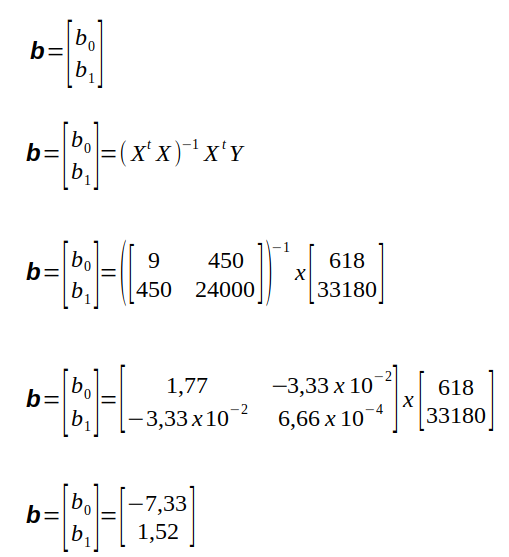
A matriz “B” representa os valores de b0 e b1 que são as “estimativas” de β0 e β1, respectivamente.
E o modelo empírico, descrito na equação S.1, para descrever a variação do rendimento da reação com a temperatura, pode ser escrito como na equação S.3.
Equação S.3. Modelo empírico “linear” para descrever a variação do rendimento da reação com a temperatura.
ŷi = -7,33 + 1,52 × ti
A equação S.3 também pode ser representada na forma matricial (Ŷ = Xb) como mostra a figura S.4.
Equação S.4. Equação matricial para o cálculo da matriz dos “rendimentos previstos” (Ŷ) pela multiplicação da matriz das temperaturas (X) pela matriz dos parâmetros (b).
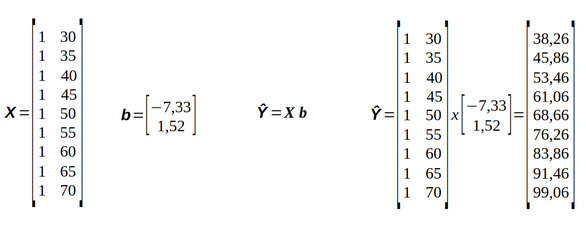
E a implementação do cálculo com o Python através do comando (representando a matriz Ŷ pela variável Y_est) :
>>> Y_est = np.dot(X,B)
>>> Y_est
array([[38.26666667],
[45.86666667],
[53.46666667],
[61.06666667],
[68.66666667],
[76.26666667],
[83.86666667],
[91.46666667],
[99.06666667]])
A diferença entre os valores previstos (Y_est) e os valores experimentais (Y_exp) correspondem aos “resíduos” (E).
>>> E = Y_exp - Y_est
>>> E
array([[-14.26],
[ -5.86],
[ 6.54],
[ 8.94],
[ 8.34],
[ 9.74],
[ 7.14],
[ -5.46],
[-15.06]])
Para avaliar a “qualidade do ajuste” de qualquer modelo deve-se verificar se os “resíduos” gerados pelo modelo são pequenos.
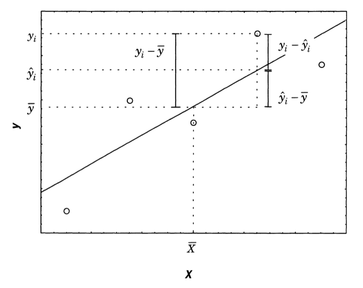
O desvio de uma resposta individual (yi) em relação à média das respostas observadas (ymedio) (Figura S.6) é formado pelos componentes:
(ŷ − ymedio) - desvio de previsão feito pelo modelo
(yi − ŷ) - diferença entre o valor observado e o valor previsto (deve ser pequena em um bom modelo)
(yi − ymedio) = (yi − ŷ) + (ŷ − ymedio)
Figura S.6. Decomposição do desvio de uma observação em relação à média global. (Fonte: Como fazer experimentos, 2001)
Elevando a equação ao quadrado e fazendo o somatório em todos os pontos:
Σ(yi − ymedio)2 = Σ[(yi − ŷ) + (ŷ − ymedio)]2
chega-se à equação:
Σ(yi − ymedio)2 = Σ(yi − ŷ)2 + 2 × Σ(yi − ŷ) × (ŷ − ymedio) + Σ(ŷ − ymedio)2
Mas como:
Σ(yi − ŷ) × (ŷ − ymedio) = 0
chega-se à equação:
Σ(yi − ymedio)2 = Σ(yi − ŷ)2 + Σ(ŷ − ymedio)2
Esses somatórios são chamados de “somas quadráticas” (SQ), e por isso a equação pode ser representada como:
SQ em torno da média = SQ residual + SQ devido à regressão
ou
SQT = SQr + SQR
Ou seja, parte da variação total das observações (yi) em torno da média (ymedio) é devida à regressão ( SQR = Σ(ŷ − ymedio)2) e parte é devida aos resíduos (SQr = Σ(yi − ŷ)2 )
E portanto quanto maior for o percentual de contribuição devido à regressão na soma quadrática total melhor será o “ajuste do modelo”, cujo índice é chamado de “coeficiente de determinação” (R2):
R2 = SQR / SQT
O valor máximo de R2 é 1, quando toda a variação em torno da média for devida ao modelo de regressão (ou explicada pelo modelo de regressão), ou seja, SQr = Σ(yi − ŷ)2 = 0.
O número de graus de liberdade da soma quadrática total (νT) deve ser igual à soma dos graus de liberdade da regressão (νR) e do resíduo (νr):
νT = νr + νR
O número de graus de liberdade da regressão νR é igual ao número de parâmetros p (β0, β1 ...) menos 1:
νR = p − 1
E o número de graus de liberdade da soma quadrática residual (νr) é a diferença entre o número de observações (n) e o número de parâmetros (p):
νr = n − p
E como o número de graus de liberdade da soma quadrática total (νT) é n − 1 temos a relação geral:
νT = νr + νR
(n − 1) = (n − p) + (p − 1)
No caso de uma regressão com dois parâmetros (β0 e β1) teríamos:
(n − 1) = (n − 2) + 1
Esses parâmetros são importantes para montar a “Tabela de Análise de Variância” (ANOVA - Analysis of Variance), que fornece informações sobre os níveis de variabilidade em um modelo de regressão e formam a base para “testes de significância”.
Para montar a tabela de ANOVA dividimos as Somas Quadráticas SQR (Σ(ŷ − ymedio)2) e SQr (Σ(yi − ŷ)2) pelos respectivos Graus de Liberdade (νR = p − 1) e (νr = n − p) e obtemos as respectivas Médias Quadráticas:
Tabela S.2. Tabela de análise de variância (ANOVA) para o ajuste de um modelo (Fonte: Como fazer experimentos, 2001)
Admitindo que os erros seguem uma distribuição normal podemos usar a tabela de ANOVA para fazer uma análise da “Significância Estatística da Regressão”.
Quando β1 = 0, isto é, quando não há relação entre x e y, pode-se demonstrar que a razão entre as médias quadráticas MQR e MQr segue uma distribuição “F”:
MQR / MQr ≈ Fp-1, n-p
Onde p − 1 é o número de graus de liberdade da Média Quadrática devida à Regressão (νR - MQR) e n − p é o número de graus de liberdade da Média Quadrática Residual (νr).
Para avaliar a significância da regressão é feito o Teste de Hipóteses:
H0 - Hipótese nula: β0 = β1 = βi = 0
H1 - Hipótese alternativa: β0, β1 ... ≠ 0
Pela “Hipótese nula” NÃO existe relação linear estatísticamente significativa entre x e y.
E pela “Hipótese alternativa” existe uma relação linear estatísticamente significativa entre x e y.
O teste consiste basicamente em “rejeitar” ou “não rejeitar” a “Hipótese nula”.
A análise é feita calculando-se a razão MQR/MQr e comparando o resultado com o valor de F tabelado para p − 1 e n − p graus de liberdade, no nível de confiança desejado. (Não confundir que na tabela de distribuição F a confiança de 95% é indicada pela percentagem de 5%)
Se a razão MQR/MQr for maior do que Fp − 1, n − p
MQR/MQr > F p − 1, n − p
deve-se descartar a possibilidade de que β0 = β1 = βi = 0, ou seja, a hipótese nula é “rejeitada”.
Ou seja, teremos evidência de que existe uma relação linear estatísticamente significativa entre x e y.
Quanto maior a razão MQR/MQr em relação a Fp − 1, n − p, mais evidente se torna a relação.
Dica
Uma limite prático para aceitar a significância é se o valor de MQR/MQr for, pelo menos, dez vezes o valor do ponto da distribuição F com o número apropriado de graus de liberdade e no nível de confiança escolhido.
A Média Quadrática Residual MQr pode, também, ser interpretada como uma medida aproximada do erro médio quadrático (s2) associado ao uso da equação de regressão para prever a resposta yi correspondente a um dado valor xi.
Quando Xa = Xmédio, o erro padrão da estimativa ŷ assume seu valor mínimo. E à medida que nos afastamos desse ponto, em qualquer direção, o erro vai aumentando. Quanto mais longe estivermos de Xa = Xmédio, mais incertas serão as previsões feitas a partir da regressão.
E portanto os limites do intervalo de confiança da previsão ŷ variam ao longo da reta de regressão formando “hipérboles”.
Lembrando que para a Análise de Variância (ANOVA) precisamos calcular as “Somas Quadráticas”:
SQ_em_torno_da_média = SQ_devido_à_regressão + SQ_residual
SQ_T = SQ_R + SQ_r
Implementando em Python o cálculo da Soma Quadrática devida à regressão SQ_R:
>>> SQ_R = np.sum( ( Y_est - np.mean(Y_exp) )**2 ) >>> SQ_R 3465.5999999999985
E a soma quadrática residual (devida aos resíduos) SQ_r:
>>> SQ_r = np.sum( (Y_exp - Y_est)**2 ) >>> SQ_r 832.4000000000004
E a Soma Quadrática Total (SQ_T) é simplesmente a soma SQ_R + SQ_r, mas também pode ser calculada pelo comando:
>>> SQ_T = np.sum( (Y_exp - np.mean(Y_exp) )**2 ) >>> SQ_T 4298.0
O número de Graus de Liberdade da Regressão (GL_R = p − 1), onde p = número de parâmetros, é feito com o comando:
>>> GL_R = b.size - 1 >>> GL_R 1
E o número de Graus de Liberdade da Soma Quadrática residual (GR_r = n − p), onde n = número de linhas da matriz X e p = número de parâmetros, é feito com o comando:
>>> GL_r = X.shape[0] - b.size >>> GL_r 7
Com os valores de SQ_R e GL_R podemos calcular a Média Quadrática da Regressão (MQ_R):
>>> MQ_R = SQ_R / GL_R >>> MQ_R 3465.5999999999985
E a Média Quadrática Residual (MQ_r):
>>> MQ_r = SQ_r / GL_r >>> MQ_r 118.91428571428578
A Média Quadrática Residual (MQ_r) pode também ser interpretada como uma medida aproximada do Erro Médio Quadrático (s2), com 7 Graus de Liberdade (GL_r), associado ao uso da equação de regressão para prever a resposta yi correspondente a um dado valor xi.
Para o “Teste de Hipótese” precisamos calcular primeiro a razão MQ_R / MQ_r, que corresponde ao F calculado (F_calc):
>>> F_calc = MQ_R / MQ_r >>> F_calc 29.14368092263332
E determinar o valor de F tabelado (F_tab) para 1 Grau de Liberdade devido à regressão (GL_R) e 7 Graus de Liberdade devido aos resíduos (GL_r), com 95% de confiança, usando o comando f.ppf(q=0.95, dfn=GL_R, dfd=GL_r).
>>> F_tab = f.ppf(q=0.95, dfn=GL_R, dfd=GL_r) Traceback (most recent call last): File "<stdin>", line 1, in <module> NameError: name 'f' is not defined
O comando retornou uma mensagem de erro declarando que “f” não está definido. Esse erro foi gerado porque me esqueci de carregar o módulo scipy.stats.
Então carregamos a módulo e executamos novamente o comando:
>>> from scipy.stats import f >>> F_tab = f.ppf(q=0.95, dfn=GL_R, dfd=GL_r) >>> F_tab 5.591447851220738
E implementamos um teste if com base na “regra prática” (heurística) de considerar como critério mínimo de significância uma diferença de 10 vezes entre F_calc e F_tab.
>>> if F_calc > (10*F_tab):
print ("F_calc > 10 * F_tab")
print ("Deve-se rejeitar a hipótese nula (b0 = b1 = bi = 0).")
print ("Ou seja, temos evidência de que existe uma relação linear estatisticamente significativa entre x e y. (b0, b1... != 0)")
else:
print ("Não se rejeita a hipótese nula (b0 = b1 = bi = 0).")
print ("Ou seja, NÃO temos evidência de que existe uma relação linear estatisticamente significativa entre x e y.")
Como o valor de F_calc (29.14) é menor do que 10 vezes F_tab (55.91), não se pode rejeitar a hipótese nula e consequentemente não existe evidência de uma relação linear “estatísticamente significativa” entre x e y.
Não se rejeita a hipótese nula (b0 = b1 = bi = 0). Ou seja, NÃO temos evidência de que existe uma relação linear estatisticamente significativa entre x e y. >>>
Se o verdadeiro valor médio de yi é β0 + β1xi, é de se esperar que observações repetidas no mesmo ponto xi se distribuam simetricamente em torno de β0 + β1xi, com desvios positivos sendo tão freqüentes quanto desvios negativos, de tal maneira que a média dos erros εi seja zero.
Num dado xi os erros em yi se distribuirão com uma certa variância σi2, que em princípio também varia com xi.
Mas para se calcular o intervalo de confiança das estimativas dos parâmetros (β0, β1 ...) serão consideradas as seguintes hipóteses: (Fonte: Como fazer experimentos, 2001)
A variância dos erros é constante ao longo de toda a faixa estudada, e igual a um certo valor σi2. A esta hipótese costuma-se dar o nome de “homoscedasticidade” das respostas observadas.
Os erros correspondentes a respostas observadas em valores diferentes da variável independente não são correlacionados, isto é, Cov(εi,εj) = O, se i ≠ j.
Os erros seguem uma distribuição normal. Na maioria dos experimentos esta é uma boa aproximação, graças ao teorema do limite central e ao esforço que todo pesquisador faz para eliminar de suas experiências os erros sistemáticos.
Estas três hipóteses sobre o comportamento dos erros aleatórios podem ser resumidas nas expressões:
εi ≊ N(0, σ2) e Cov(εi,εj) = 0
Com base nessas suposições pode-se dar prosseguimento ao cálculo do “intervalo de confiança” para os parâmetros do modelo.
Os intervalos de confiança dos parâmetros podem ser calculados pela equação S.5
Equação S.5. Equação para o cálculo do intervalo de confiança dos parâmetros do modelo
bi ± tn − p × (Erro Padrão de bi)
Admitindo que o valor de s2, a variância residual em torno da regressão corresponde à Média Quadrática Residual (MQr calculada na tabela ANOVA), seja uma boa estimativa de σ2, podemos obter uma estimativa do erro padrão de bi.
Como também se admite que os erros se distribuem normalmente, pode-se usar a distribuição de Student para testar a significância do valor estimado para bi.
O número de graus de liberdade do valor de t é n − p, que é o número de graus de liberdade da estimativa s2 (MQs, e conseqüentemente também do erro padrão.
O uso de matrizes facilita sobremaneira o cálculo dos “erros padrão” dos parâmetros. E isso é feito pelo cálculo da “Matriz de Covariância” dos parâmetro como mostra a figura S.7
E essa matriz pode ser calculada pela equação S.6
Equação S.6. Equação para o cálculo da matriz de covariância dos parâmetros do modelo
V(B) = (XtX)−1 σ2
Essa é outra equação muito importante, que se aplica ao ajuste por mínimos quadrados de qualquer modelo “linear nos parâmetros”, dentro das suposições que foram feitas no início desta seção.
Multiplicando a matriz (XtX)−1 pela Média Quadrática Residual (MQr), como estimativa de σ2, e tirando a raiz quadrada dos elementos da diagonal principal, obtemos os erros padrão dos parâmetros (b0, b1 ...).
Nota
Lembre-se que estamos dando continuidade aos comandos já executados anteriormente!
Cálculo da Matriz de Covariância:
>>> matriz_covar = inv_X_t_dot_X * MQ_r
>>> matriz_covar
array([[ 2.11403175e+02, -3.96380952e+00],
[-3.96380952e+00, 7.92761905e-02]])
A diagonal da Matriz de Covariância corresponde às variâncias das estimativas dos parâmetros. (V(b0), V(b1) ...):
>>> V_B = np.diag(matriz_covar) >>> V_B array([2.11403175e+02, 7.92761905e-02])
E a raiz quadrada das variâncias das estimativas dos parâmetros corresponde aos erro padrão das estimativas dos parâmetros (s(b0), s(b1) ...).
>>> erro_padrao_B = np.sqrt(V_B) >>> erro_padrao_B array([14.53971027, 0.28156028])
O valor de t crítico é calculado para o número de Graus de Liberdade da Soma Quadrática residual (GL_r) e no nível de 95%s de confiança.
Mas antes precisamos carregar o módulo scipy.stats para o cálculo do valor tabelado de t de Student.
>>> from scipy.stats import t >>> t_crit = t.ppf(0.95, GL_r) >>> t_crit 1.894578605061305
E o loop que foi implementado para o cálculo do intevalo de confiança e avaliação da significância estatística dos parâmetros da regressão.
i = 0
for par_b, erro_b in zip(B, erro_padrao_B):
print("Parâmetro: %f e Erro: %f" % (par_b.item(), erro_b))
intervalo = t_crit * erro_b
print ("Intervalo: ", intervalo)
b_max = par_b.item() + intervalo
b_min = par_b.item() - intervalo
print("Intervalo de confiança do parâmetro b%d (%f), limite superior (%f) e limite inferior (%f)" % (i, par_b.item(), b_max, b_min))
print ("Isto significa que há 95%s de probabilidade de que o verdadeiro valor do parâmetro b%d esteja entre %f e %f" % ('%', i, b_min, b_max))
if abs(intervalo) > abs(par_b.item()):
print ("Como esses dois limites têm sinais contrários, e como nenhum valor num intervalo de confiança é mais provável do que outro, pode ser que o verdadeiro valor de b%d seja zero. Ou seja, o valor de b%d = %f não é estatisticamente significativo e portanto não existe evidência suficiente para manter o termo b%d no modelo." % (i, i, par_b.item(), i))
print()
i += 1
O qual gerou a saída:
Parâmetro: -7.333333 e Erro: 14.539710 Intervalo: 27.546623992708057 Intervalo de confiança do parâmetro b0 (-7.333333), limite superior (20.213291) e limite inferior (-34.879957) Isto significa que há 95% de probabilidade de que o verdadeiro valor do parâmetro b0 esteja entre -34.879957 e 20.213291 Como esses dois limites têm sinais contrários, e como nenhum valor num intervalo de confiança é mais provável do que outro, pode ser que o verdadeiro valor de b0 seja zero. Ou seja, o valor de b0 = -7.333333 não é estatisticamente significativo e portanto não existe evidência suficiente para manter o termo b0 no modelo. Parâmetro: 1.520000 e Erro: 0.281560 Intervalo: 0.5334380798399798 Intervalo de confiança do parâmetro b1 (1.520000), limite superior (2.053438) e limite inferior (0.986562) Isto significa que há 95% de probabilidade de que o verdadeiro valor do parâmetro b1 esteja entre 0.986562 e 2.053438
Como estes dois limites do parâmetro b0 têm sinais contrários, e como nenhum valor num intervalo de confiança é mais provável do que outro, pode ser que o verdadeiro valor de b0 seja zero. Em outras palavras, o valor b0 = −7.33 não é estatisticamente significativo, e portanto não existe evidência suficiente para mantermos o termo b0 no modelo.
Como pode ser visto no gráfico da figura S.2 não e possivel traçar uma reta que passe por todos os pontos experimentais.
Por isso vamos modelar a influência da temperatura sobre o rendimento com um modelo quadrático como mostra a equação S.7
Equação S.7. Modelo empírico quadrático para descrever a variação do rendimento da reação com a temperatura.
yi = β0 + β1×ti + β2×ti2 + εi
O ajuste deste novo modelo aos valores experimentais também é feito por meio da equação matricial S.2. Mas agora as matrizes precisam ser expandidas para se ajustarem à equação quadrática S.7 como mostra a figura S.8.
Figura S.8. Equação matricial representando o sistema de 9 equações do modelo empírico “quadrático” que descreve a relação rendimento e temperatura descrita na tabela S.1 (Fonte: Como fazer experimentos, 2001)
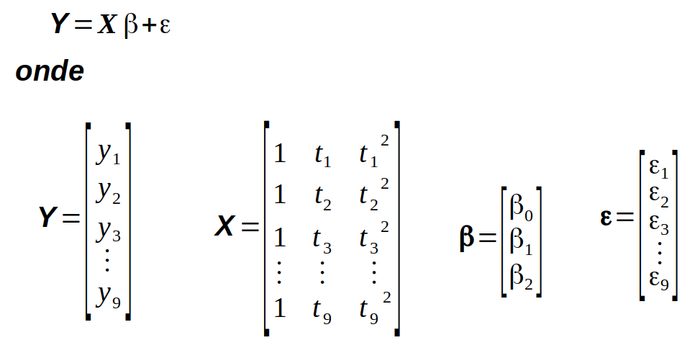
Neste caso a matriz “X” pode ser montada incluindo a coluna correspondente a “t2” com os comandos:
>>> X = np.array([[30, 35, 40, 45, 50, 55, 60, 65, 70]])
>>> X
array([[30, 35, 40, 45, 50, 55, 60, 65, 70]])
>>> X = X.T
>>> X
array([[30],
[35],
[40],
[45],
[50],
[55],
[60],
[65],
[70]])
>>> X = np.hstack([np.ones(X.shape), X, X**2])
>>> X
array([[1.000e+00, 3.000e+01, 9.000e+02],
[1.000e+00, 3.500e+01, 1.225e+03],
[1.000e+00, 4.000e+01, 1.600e+03],
[1.000e+00, 4.500e+01, 2.025e+03],
[1.000e+00, 5.000e+01, 2.500e+03],
[1.000e+00, 5.500e+01, 3.025e+03],
[1.000e+00, 6.000e+01, 3.600e+03],
[1.000e+00, 6.500e+01, 4.225e+03],
[1.000e+00, 7.000e+01, 4.900e+03]])
>>>
Aplicando a equação S.2, conforme os comandos descritos anteriormente, obtemos a matriz “b” com os parâmetros da equação de regressão:
>>> Y_exp = np.array([[24], [40], [60], [70], [77], [86], [91], [86], [84]])
>>> X_t = X.T
>>> X_t_prod_matricial_X = np.dot(X_t,X)
>>> inv_X_t_dot_X = np.linalg.inv(X_t_prod_matricial_X)
>>> X_t_Y_exp = np.dot(X_t,Y_exp)
>>> b = np.dot(inv_X_t_dot_X, X_t_Y_exp)
>>> b
array([[-1.58242424e+02],
[ 7.98753247e+00],
[-6.46753247e-02]])
O que significa que o modelo quadrático estima os rendimentos por meio da equação S.8.
Equação S.8. Modelo empírico “quadrático” para descrever a variação do rendimento da reação com a temperatura.
ŷi = − 158,242424 + 7.98753247 × ti − 0,0646753247 × ti2
A figura S.9 mostra o gráfico da equação S.8, onde se observa que o ajuste é muito melhor do que o modelo linear (Figura S.2).
Figura S.9. Gráfico com os resultados experimentais da tabela S.1 e a curva de regressão do modelo quadrático.(Gráfico feito com o programa Calc)
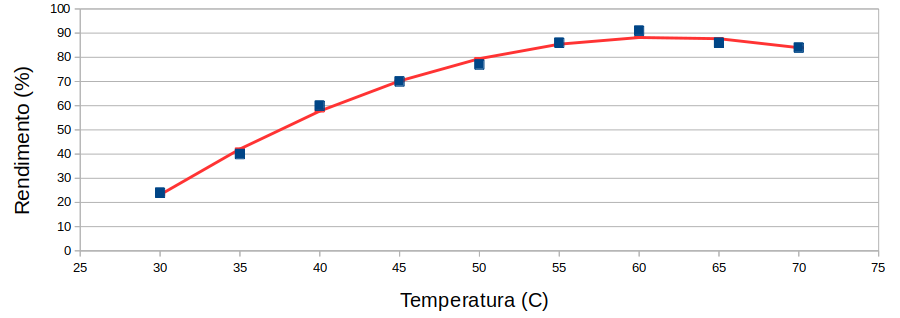
Os cálculos da tabela ANOVA para avaliar a Significância Estatística da Regressão foram feitos com os seguintes comandos:
>>> Y_est = np.dot(X, b)
>>> SQ_R = np.sum( ( Y_est - np.mean(Y_exp) )**2 )
>>> SQ_T = np.sum( (Y_exp - np.mean(Y_exp) )**2 )
>>> SQ_r = np.sum( (Y_exp - Y_est)**2 )
>>> GL_R = b.size - 1
>>> GL_r = X.shape[0] - b.size
>>> MQ_R = SQ_R / GL_R
>>> MQ_r = SQ_r / GL_r
>>> F_calc = MQ_R / MQ_r
>>> from scipy.stats import f
>>> F_tab = f.ppf(q=0.95, dfn=GL_R, dfd=GL_r)
>>> if F_calc > (10*F_tab):
... print ("F_calc > 10 * F_tab")
... print ("Deve-se rejeitar a hipótese nula (b0 = b1 = bi = 0).")
... print ("Ou seja, temos evidência de que existe uma relação linear estatisticamente significativa entre x e y. (b0, b1... != 0)")
... else:
... print ("Não se rejeita a hipótese nula (b0 = b1 = bi = 0).")
... print ("Ou seja, NÃO temos evidência de que existe uma relação linear estatisticamente significativa entre x e y.")
...
F_calc > 10 * F_tab
Deve-se rejeitar a hipótese nula (b0 = b1 = bi = 0).
Ou seja, temos evidência de que existe uma relação linear estatisticamente significativa entre x e y. (b0, b1... != 0)
E forneceram os seguintes valores:
Média Quadrática da Regressão MQ_R = SQ_R / GL_R = 2135.403896104082
Média Quadrática Residual MQ_r = SQ_r / GL_r = 4.532034632034644
Erro Médio Quadrático s2 (4.532035) com 6 Graus de Liberdade.
F_calc para o teste de significância da regressão: 471.17995988159487
F tabelado (5.143253) para 2 graus de liberdade do numerador e 6 graus de liberdade no denominador.
Através dos quais foi possível “evidenciar estatísticamente” a significância estatística do modelo quadrático:
Como F_calc > 10 * F_tab, deve-se rejeitar a hipótese nula (b0 = b1 = b2 = 0). Ou seja, temos evidência de que existe uma relação linear estatisticamente significativa entre x e y. (b0, b1 e b2 ≠ 0).
Foram executados os seguintes comandos iniciais:
#Matriz de Covariância (matriz_covar): >>> matriz_covar = inv_X_t_dot_X * MQ_r #A diagonal da Matriz de Covariância corresponde às variâncias das estimativas dos parâmetros. (V(b0), V(b1 e V(b2) ...) >>> V_b = np.diag(matriz_covar) #Erros padrão dos parâmetros: >>> erro_padrao_b = np.sqrt(V_b) #O valor t crítico (t_crit) é calculado para o número de Graus de Liberdade da Soma Quadrática residual (GL_r) e no nível de 95% de confiança: >>> from scipy.stats import t >>> t_crit = t.ppf(0.95, GL_r)
E o loop para o cálculo do intervalo de confiança dos parâmetros:
>>> i = 0
>>> for par_b, erro_b in zip(b, erro_padrao_b):
... print("Parâmetro: %f e Erro: %f" % (par_b.item(), erro_b))
... intervalo = t_crit * erro_b
... print ("Intervalo: ", intervalo)
... b_max = par_b.item() + intervalo
... b_min = par_b.item() - intervalo
... print("Intervalo de confiança do parâmetro b%d (%f), limite superior (%f) e limite inferior (%f)" % (i, par_b.item(), b_max, b_min))
... print ("Isto significa que há 95%s de probabilidade de que o verdadeiro valor do parâmetro b%d esteja entre %f e %f" % ('%', i, b_min, b_max))
... if abs(intervalo) > abs(par_b.item()):
... print ("Como esses dois limites têm sinais contrários, e como nenhum valor num intervalo de confiança é mais provável do que outro, pode ser que o verdadeiro valor de b%d seja zero. Ou seja, o valor de b%d = %f não é estatisticamente significativo e portanto não existe evidência suficiente para manter o termo b%d no modelo." % (i, i, par_b.item(), i))
... print()
... i += 1
...
O qual gerou a saída:
Parâmetro: -158.242424 e Erro: 11.672005 Intervalo: 22.680810531882145 Intervalo de confiança do parâmetro b0 (-158.242424), limite superior (-135.561614) e limite inferior (-180.923235) Isto significa que há 95% de probabilidade de que o verdadeiro valor do parâmetro b0 esteja entre -180.923235 e -135.561614 Parâmetro: 7.987532 e Erro: 0.488315 Intervalo: 0.9488844520661023 Intervalo de confiança do parâmetro b1 (7.987532), limite superior (8.936417) e limite inferior (7.038648) Isto significa que há 95% de probabilidade de que o verdadeiro valor do parâmetro b1 esteja entre 7.038648 e 8.936417 Parâmetro: -0.064675 e Erro: 0.004852 Intervalo: 0.009428537605566101 Intervalo de confiança do parâmetro b2 (-0.064675), limite superior (-0.055247) e limite inferior (-0.074104) Isto significa que há 95% de probabilidade de que o verdadeiro valor do parâmetro b2 esteja entre -0.074104 e -0.055247 >>>
A contrário do modelo linear, todos os parâmetros do modelo quadrático são “estatísticamente significativos” (≠ 0). E portanto devem permanecer no modelo.
Como vimos, os testes estatísticos de “Significância da Regressão” e “Intervalo de Confiança dos Parâmetros” permitem decidir pela aceitação ou rejeição de um modelo com base em critérios quantitativos e portanto “objetivos”.
Nota
O programa usado neste tutorial está disponível para download no link regressao_linear_03.py.
S.1.5. Usando a biblioteca Matplotlib para exibir gráficos.
Matplotlib é uma biblioteca Python especializada no desenvolvimento de gráficos bi e tridimensionais.
A primeira etapa é carregar a biblioteca:
import matplotlib.pyplot as plt
E executar os comandos:
>>> Y_exp = np.array([[24], [40], [60], [70], [77], [86], [91], [86], [84]])
>>> X = np.array([[30, 35, 40, 45, 50, 55, 60, 65, 70]])
>>> X = X.T
>>> X = np.hstack([np.ones(X.shape), X, X**2])
>>> X_t = X.T
>>> X_t_prod_matricial_X = np.dot(X_t,X)
>>> inv_X_t_dot_X = np.linalg.inv(X_t_prod_matricial_X)
>>> X_t_Y_exp = np.dot(X_t,Y_exp)
>>> b = np.dot(inv_X_t_dot_X, X_t_Y_exp)
>>> Y_est = np.dot(X,b)
>>> X_col_2 = X[:,1]
>>> import matplotlib.pyplot as plt
>>> plt.scatter(X_col_2, Y_exp, c='blue')
>matplotlib.collections.PathCollection object at 0x7f677420b160>
>>> plt.plot(X_col_2, Y_est, c='r')
[>matplotlib.lines.Line2D object at 0x7f678ad62ef0>]
>>> plt.xlabel('Temperatura (C)')
>matplotlib.text.Text object at 0x7f67750a33c8>
>>> plt.ylabel('Rendimento (%)')
>matplotlib.text.Text object at 0x7f67750bc1d0>
>>> plt.title('Gráfico com dados experimentais do rendimento em função da temperatura ')
>matplotlib.text.Text object at 0x7f6774260ac8>
>>> plt.show()
Vamos lembrar que os valores de temperatura (variável independente) foram organizados, tanto no modelo linear quanto no modelo quadrático, na segunda coluna da matriz (array) X. Por isso a segunda coluna foi extraída (slice) com o comando X_col_2 = X[:,1] e armazenada na variável X_col_2.
Com os comandos acima foi possível obter o gráfico dos dados experimentais e da regressao do modelo quadrático como mostra a figura S.10.
Figura S.10. Gráfico gerado com a biblioteca Matplotlib a partir dos dados da tabela S.1 e os dados gerados pelo modelo de regressão quadrático.
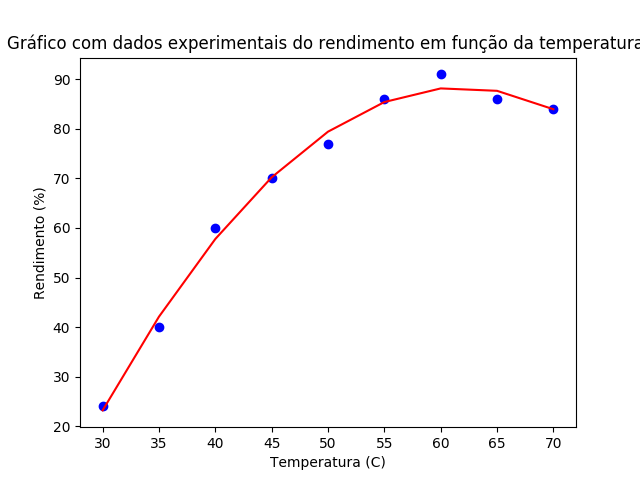
Mas também pode ser usado o método plot para exibir pontos ao invés de linhas.
plt.plot(X_col_2, Y_exp, 's', c='blue')
O terceiro argumento “s” define que seja usado o símbolo quadrado (square) para representar os pontos experimentais.
Também podemos criar o gráfico dos “resíduos” (y_exp - y_est) com os comandos:
#Ajuste do tamanho
plt.figure(figsize=(10,5))
#Cria subplot com separação horizontal
plt.subplot(1,2,1)
plt.plot(X_col_2, Y_exp, 's', c='red')
plt.plot(X_col_2, Y_est, c='blue')
plt.xlabel('Temperatura (C)')
plt.ylabel('Rendimento (%)')
plt.title('Dados experimentais')
plt.subplot(1,2,2)
plt.axis([20, X_col_2[-1]+10, -10, 10])
plt.plot(X_col_2, E, 's', c='blue')
plt.hlines(y=0, xmin=20, xmax=X_col_2[-1]+10, color='red')
#Aumentar espaço entre os gráficos
plt.subplots_adjust(wspace=0.4)
plt.show()
Os dois gráficos são exibidos na mesma janela como mostra a figura: S.11.
Figura S.11. No lado esquerdo o gráfico gerado a partir dos dados da tabela S.1 e os dados gerados pelo modelo de regressão quadrático. E no lado direito os dados dos resíduos.
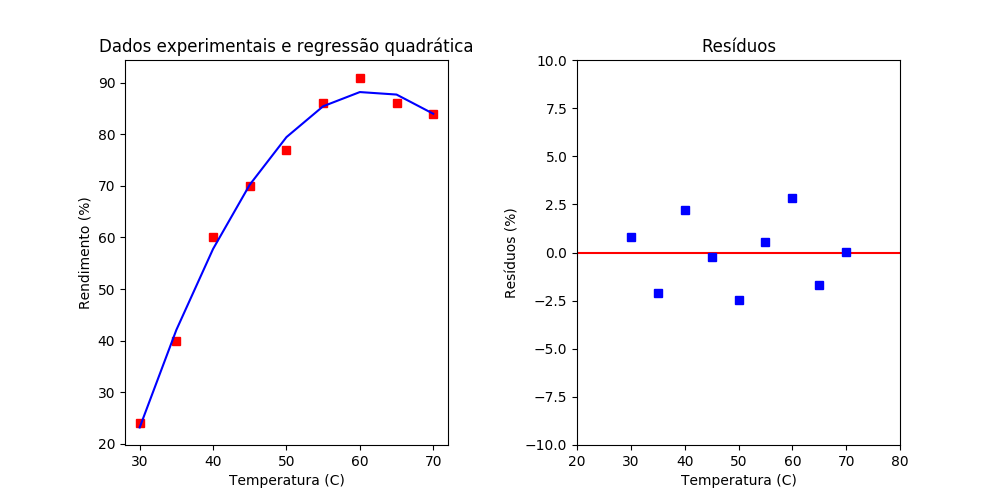
Também podemos adicionar um terceiro gráfico mostrando a “correlação” entre os resultados observados e simulados como mostra a figura S.12.
Figura S.12. No lado esquerdo o gráfico gerado a partir dos dados da tabela S.1 e os dados gerados pelo modelo de regressão quadrático. No centro os dados dos resíduos. E à direita o gráfico com os dados observados e simulados
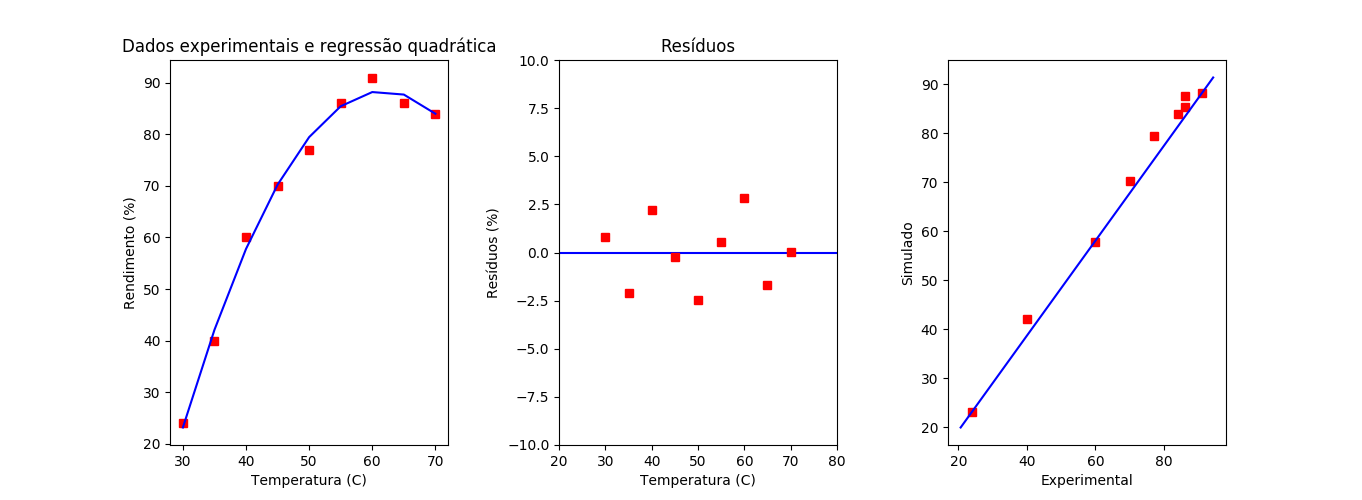
Para exibir o terceiro gráfico com os resultados simulados e observados usamos os comandos adicionais:
plt.subplot(1,3,3)
plt.plot(Y_exp, Y_est, 's', c='red')
#Dica
#https://stackoverflow.com/questions/40516661/adding-line-to-scatter-plot-using-pythons-matplotlib
x_lim = plt.xlim()
y_lim = plt.ylim()
plt.plot(x_lim, y_lim, c='blue')
plt.xlabel('Experimental')
plt.ylabel('Simulado')
#Aumentar espaço entre os gráficos
plt.subplots_adjust(wspace=0.4)
S.1.6. Usando a biblioteca Pandas para acessar e processar dados
Para usar a biblioteca é necessário primeiro “carregar” com o comando:
>>> import pandas as pd
Criamos um arquivo arq_Temp_Rend.csv contendo os valores de Temperatura e Rendimento:
T,R 30,24 35,40 40,60 45,70 50,77 55,86 60,91 65,86 70,84
Para abrir o arquivo usamos o comando read_csv:
data = pd.read_csv('arq_Temp_Rend.csv', sep=',')
Mas data é uma variável do tipo “DataFrame”:
>>> type(data) <class 'pandas.core.frame.DataFrame'>
Por isso fiz primeiro a conversão para o tipo “array” para realizar as operações matriciais com NumPy.
X = data.values[:,0] X = X.reshape(-1,1) Y_exp = data.values[:,1] Y_exp = Y_exp.reshape(-1,1)
Nota
Conforme a mensagem do Stackoverflow Convert pandas dataframe to NumPy array o método values será removido em futuras versões do Pandas.
Por isso seria recomendável usar o métod to_numpy().
Mas no momento estou usando a versão do Pandas 0.19.2, que não possui o método to_numpy(), e por isso usei o método values.
Além disso o método as_matrix foi removido desde a versão 0.23.0 do Pandas.
Mas fica registrado o lembrete. ;-)