Dica
Além de polivalentes precisamos ser multivariados.
Os diferentes ambientes em que transitamos (Natural, Artificial ou Cultural) apresentam características multivariadas ou multifatoriais.
Ou seja, os processos e transformações que ocorrem nesses diferentes ambientes são “efeitos” resultantes de diferentes causas (correlacionadas ou independentes).
E esses “efeitos”, por sua vez, são também “causas” de outros efeitos, em uma rede infindável de “causas & consequências”.
“Captamos” uma parcela dessa “Realidade Maior” e construímos uma “Realidade Fenomenológica” a partir dos dados gerados apenas pelos nossos sentidos ou expandidos com o uso de instrumentos.
Esse processo tem se acelerado de maneira exponencial gerando um “oceano de dados” que demanda o uso de ferramentas adequadas para a sua “interpretação eficiente e eficaz”.
Mas o nosso pensamento “intuitivo” é “univariado”, e tentamos interpretar e compreender uma realidade que é “multivariada”.
Então o que fazer?
Aí entra em cena a importância da “Ciência Estatística” que fornece ferramentas que auxiliam a “extrair blocos de informações” a partir de dados “multivariados”. Para “construir conhecimentos” pela justaposição criteriosa desses “blocos informacionais”.
Nota
Neste caso, nos referimos à construção de um “conhecimento probabilístico” como “complemento” ao “conhecimento determinístico”. Sem nos esquecer da importância do “conhecimento heurístico”.
Reagrupei, de forma livre e simplificada, os tipos “oficiais” de conhecimento nos 3 tipos citados: probabilístico, determinístico e heurístico. ;-)
Vamos nesta seção discutir alguns conceitos e técnicas de “Análise Estatística Multivariada”.
Na área da Química essas técnicas são agrupadas na ciência conhecida por Quimiometria, que pode ser definida como:
“O emprego de técnicas estatísticas, matemáticas e gráficas para resolver problemas químicos”. (Fonte: Como fazer experimentos, 2001)
Mas atualmente essas técnicas estão sendo mais popularmente conhecidas na área chamada de Aprendizado de máquina (Machine Learning), um ramo da Inteligência Artificial.
Me permita fazer algumas digressões sobre “Inteligência Artificial”.
Definir “Inteligência Artificial” não é uma tarefa fácil pois nem ao menos existe um consenso sobre o que seria inteligência.
Somos capazes de perceber a “inteligência” no comportamento de “entidades” (vivas ou artificiais), mas temos dificuldade para definir afinal o que é “inteligência”.
No artigo Intelligence Without Reason o pesquisador em robótica Rodney Brooks analisa os “comportamentos inteligentes” de “sistemas biológicos”, mas sem considerar a necessidade do atributo pensamento.
Logo no início do artigo o autor evita discutir o conceito de inteligência e simplesmente declara: “Prefiro ficar com uma noção mais informal de inteligência, sendo o tipo de coisa que os humanos fazem, praticamente o tempo todo.” (Fonte: Intelligence Without Reason.)
Sem a pretensão de me aprofundar nessa área, com muito mais perguntas do que respostas, gostaria apenas de lembrar do axioma:
“Todo efeito tem uma causa; todo efeito inteligente tem uma causa inteligente; a potência da causa inteligente está na razão da grandeza do efeito”. (Fonte: Revista Espírita, 1869)
Portando se encontramos sistemas biológicos com “comportamentos inteligentes” podemos considerar que esses sistemas são o efeito de uma inteligência superior.
E se considerarmos que a inteligência é um “atributo” da mente e o pensamento é uma “ação” da mente (Fonte: Relationship between intelligence, thinking and knowledge), constatamos que essa “inteligência superior” é o atributo de uma “mente superior” e consequentemente com uma capacidade de pensamento proporcionalmente superior.
Voltando para o nosso ponto de partida, Análise Estatística Multivariada, dissemos que é uma técnica (ou melhor, um conjunto de técnicas) que faz parte do que se convencionou chamar de Aprendizado de máquina (Machine Learning).
E novamente, mais uma pequena digressão.
Uma máquina (computador) é capaz de aprender?.
O processo de aprendizagem humana envolve o ato de “pensar”.
Mas e as máquinas? “As máquinas são capazes de pensar?”.
Agora eu vou recorrer à filosofia do Garfield: Se você não encontra resposta para a sua pergunta; mude a sua pergunta!
E foi o que o grande Alan Turing fez ao substituir a pergunta:
“As máquinas são capazes de pensar?”
Pela pergunta:
“As máquinas são capazes de fazer o que (nós como entidades pensantes) podemos fazer?” (Fonte: Aprendizado de Máquina)
Podemos então definir, de maneira prática, que “Aprendizado de Máquina” (ou Machine Learning - ML) é um subconjunto de ciência da computação que envolve a aplicação de técnicas estatísticas sobre dados para gerar algum processo que pode realizar alguma tarefa. E inclui três tipos de aprendizagem: aprendizado supervisionado, aprendizado não supervisionado e aprendizado por reforço. (Fonte: How to explain machine learning in plain English)
Após essas breves considerações vamos dar prosseguimento ao tema central dessa seção: Modelos Empíricos com Regressão Linear Multivariada.
Nessa seção vamos mostrar a aplicação prática da técnica de Análise de Regressão Multivariada no desenvolvimento de Modelos Empíricos a partir de dados experimentais com muitas variáveis.
Neste caso o objetivo é encontrar uma equação matemática que permita estabelecer a relação entre uma variável “dependente” (usualmente representada por y) com várias variáveis “independentes” (usualmente reprensentada por x1, x2 ... xn).
Os dados multivariados são usualmente organizados na forma de tabela (matriz, planilha) formada por “n” linhas e “m” colunas.
Cada linha corresponde a uma “amostra” (objeto), e cada coluna corresponde a um “atributo” (propriedade, variável, parâmetro) analisado (medido) da respectiva amostra.
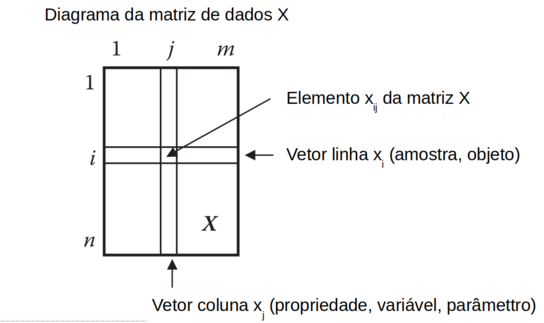
Nessa matriz, indicada por “X”, cada elemento da matriz é indicado por “xij” onde “i” é a linha, e “j” a coluna. (Figura T.1)
Figura T.1. Diagrama da matriz X, de dados multivariados, com “n” linhas (amostras, objetos) e “m” colunas (propriedades, variáveis, parâmetros, característica)
Geometricamente, cada amostra (objeto) pode ser considerado como um “ponto” em um espaço com m dimensões, onde cada dimensão (coordenada) representa uma propriedade (variável, parâmetro, característica).
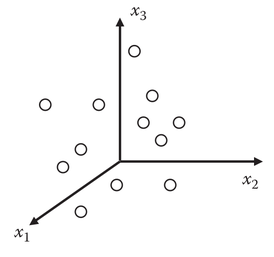
Por exemplo, a figura T.2 representa um espaço tridimensional (m=3) no qual cada coordenada (eixo) representa uma variável (x1, x2 e x3) e cada ponto no espaço representa uma amostra (objeto).
Figura T.2. Gráfico que mostra cada amostra (objeto) em um espaço 3D onde cada dimensão (x1, x2 e x3) corresponde a uma variável (propriedade, parâmetro, característica)(Fonte: Introduction to multivariate statistical analysis in chemometrics, 2009)
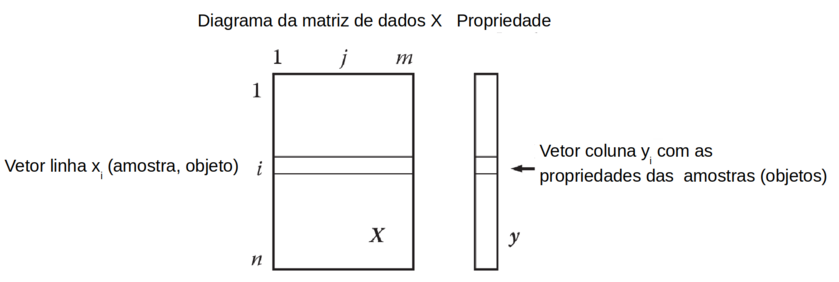
Além da matriz “X” é necessário uma matriz de uma (ou mais) coluna “Y” com as respectivas propriedades (ou rótulos) para cada amostra. (Figura T.3).
Figura T.3. Matriz “X” e a respectiva matriz coluna Y com as respectivas “propriedades” “yi” (resposta) para cada variável “xi”. As propriedades (respostas) podem ser variáveis contínuas ou discretas. (Fonte: Introduction to multivariate statistical analysis in chemometrics, 2009)
Os dados utilizados neste exemplo foram obtidos de um vídeo tutorial disponível no Youtube no link: Mod-07 Lec-32 Regression on Principal Components.
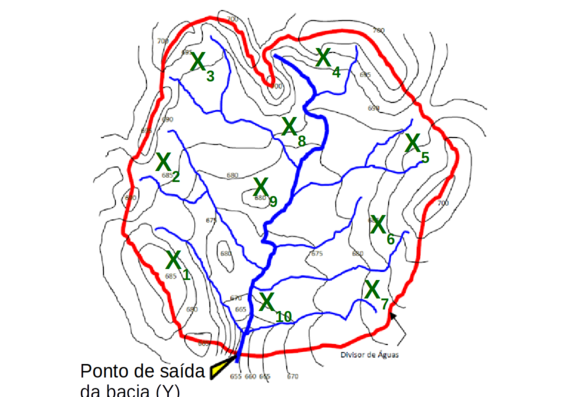
Vamos considerar uma Bacia Hidrográfica na qual existem 10 pluviômetros instalados em diferentes “tributários” da bacia (Figura T.4). E usar os registros de precipitação anual, em mm, para os 10 pluviômetros (x1, x2, x3, ... x10) e o escoamento anual no ponto de saída da bacia (exutório) para construir um modelo que permita calcular o escoamento anual total da bacia (em mm) a partir dos registros de chuva anual dos 10 pluviômetros.(Equação S.1)
Equação T.1. Modelo multivariado que descreve o volume de escoamento anual da bacia hidrográfica em função dos registros de precipitação de 10 pluviômetros (x1, x2, x3, ... x10) instalados na bacia de drenagem.
yi = β0 + β1∗x1i + β2∗x2i + β3∗x3i + β4∗x4i + β5∗x5i + β6∗x6i + β7∗x7i + β8∗x8i + β9∗x9i + β10∗x10i + εi
Figura T.4. Diagrama de uma bacia hidrográfica com 10 pluviômetros (x1, x2, x3, ... x10) em diferentes locais da bacia e ponto de saída da bacia.(Fonte: Planejamento, manejo e gestão de bacias)
O conjunto de dados (dataset) com os registros de precipitação anual dos 10 pluviômetros (x1, x2, x3, ... x10) e do escoamento anual da bacia (Y), durante 19 anos (1979-1997) estão disponíveis no arquivo rainfall.csv. (Fonte: Mod-07 Lec-32 Regression on Principal Components)
Vamos utilizar novamente a Equação matricial geral para o ajuste de modelos pela técnica dos “mínimos quadrados” para calcular os “parâmetros do modelo”.
B = (XtX)-1 XtY
Vamos montar uma matriz (X) correspondente às leituras dos 10 pluviômetros, mais uma coluna de “uns” referente à constante β0.
Inicialmente carregar as bibliotecas NumPy, Pandas e Matplotlib.
import numpy as np import pandas as pd import matplotlib.pyplot as plt
Abrir o arquivo rainfall.csv, que deve estar no diretório local.
data = pd.read_csv('rainfall.csv', sep=',')
Os dados são armazenados na variável data, do tipo “dataframe”, com a seguinte estrutura:
>>> data
Ano--------x1------x2------x3------x4------x5------x6------x7------x8------x9-----x10---------y
0 1979 1948 4177 5496 2922 5713 3640 3203 2739 2167 2299 3255.2
1 1980 2261 3670 7797 3327 6934 4424 3692 3451 2866 2653 3682.7
2 1981 1989 4353 7392 2837 6275 4827 4476 4403 3568 3241 3921.9
3 1982 1999 3307 7061 3439 6641 4815 4256 4129 3447 3046 3909.3
4 1983 2086 4230 6564 2987 6675 3959 3900 3559 4078 3583 3768.9
5 1984 1717 2714 5919 3394 5605 3648 3085 2440 2631 2587 3106.4
6 1985 1383 2357 5053 2958 5144 3106 4052 3006 3049 2890 3069.4
7 1986 1470 3004 3951 2691 5116 3557 2775 1909 1952 1723 2940.2
8 1987 1350 2446 4280 2397 4722 3556 2818 2945 2931 2733 3015.3
9 1988 1602 4188 5910 3619 6869 5142 3190 3660 3964 3107 3953.2
10 1989 1417 3631 5145 3282 5226 3793 2663 3017 2579 3367 3172.4
11 1990 1662 4683 6384 6376 7313 4679 3037 3666 3142 2621 3791.0
12 1991 1955 4553 5679 6141 6068 3651 2601 2791 2148 2448 3344.8
13 1992 1974 3836 6021 5646 5876 4026 3037 3920 2583 2742 3650.3
14 1993 2094 4183 6733 6720 6044 6573 2465 3406 2410 2539 3878.7
15 1994 3149 6128 8151 9048 8384 7467 2888 3522 2496 2895 4606.2
16 1995 1471 2952 4151 4975 5149 4733 2603 3493 3396 3554 3498.8
17 1996 1691 3711 4200 4962 5359 3782 3185 3099 3381 2938 3241.0
18 1997 2373 4836 6704 6563 6197 5001 3902 3685 3636 3365 4013.5
>>>
Para realizar as operações matriciais com os comandos do Numpy, criamos a matriz de dados X extraindo as 10 primeiras colunas da variável data, e a matriz de escoamento Y com a última coluna da variável data.
X = data.values[:,1:11] Y = data.values[:,11]
A variável X é uma matriz bidimensional de 19 linhas por 10 colunas. Mas a matriz Y é um vetor unidimensional com 19 elementos:
>>> X.shape (19, 10) >>> Y.shape (19,)
Por isso alteramos a dimensionalidade da variável Y com o comando reshape(-1,1):
>>> Y = Y.reshape(-1,1) >>> Y.shape (19, 1)
Para o cálculo da estimativa do parâmetro constante (b0) é necessário inserir uma coluna de “ums” na matriz X e para isso usamos o método ones passando como como argumento o número de linhas da matriz X com o método shape[0]:
>>> ones = np.ones(X.shape[0])
>>> ones
array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1.])
>>> ones.shape
(19,)
>>> ones = ones.reshape(-1,1)
>>> ones.shape
(19, 1)
A variável ones “aponta” para um vetor unidimensinal de “ums”, por isso usamos o método reshape(-1,1) para transformar em uma matriz com 19 linhas e 1 coluna.
A matriz ones é combinada com a matriz X usando o método hstack([ones, X]):
>>> X = np.hstack([ones, X])
A matriz transposta de X (X_t) é obtida com o método T:
>>> X_t = X.T
O produto matricial de X_t e X é obtido com o método dot(X_t,X) e armazenado na variável X_t_dot_X:
>>> X_t_dot_X = np.dot(X_t,X)
A matriz inversa de X_t_dot_X é calculada com o método linalg.inv(X_t_dot_X) e o resultado armazenado na variável inv_X_t_dot_X:
>>> inv_X_t_dot_X = np.linalg.inv(X_t_dot_X)
O segundo termo da equação é obtido pelo produto matricial das matrizes X_t e Y:
>>> X_t_dot_Y = np.dot(X_t,Y) >>> X_t_dot_Y = X_t_Y.reshape(-1,1)
E a matriz B com as estimativas dos parâmetros β0, β1 ... β10 da equação de regressão pode então ser determinada com o produto matricial:
>>> B = np.dot(inv_X_t_dot_X, X_t_Y)
>>> B
array([[ 7.82347374e+02],
[ 1.86128582e-01],
[ 4.83564765e-02],
[-1.98488741e-02],
[ 1.91236201e-03],
[ 1.19622640e-01],
[ 1.55539685e-01],
[ 2.31577538e-02],
[ 1.94764762e-01],
[ 7.99100377e-02],
[-4.08511690e-03]])
Cada elemento da matriz B é um dos coeficientes do modelo e portanto o modelo empírico “multivariado” que permite calcular o escoamento anual total da bacia (em mm) a partir dos registros de chuva anual dos 10 pluviômetros pode ser agora expresso pela equação T.2.
Equação T.2. Modelo multivariado que descreve o volume de escoamento anual da bacia hidrográfica em função dos registros de precipitação de 10 pluviômetros (x1, x2, x3, ... x10) instalados na bacia de drenagem.
yi = 782,34 + 0,1861∗x1i + 0,0483∗x2i − 0,0198∗x3i + 0,0019∗x4i + 0,1196∗x5i + 0,1555∗x6i + 0,0232∗x7i + 0,1947∗x8i + 0,0799∗x9i − 0,0041∗x10i + εi
Os valores de escoamento da bacia “estimados” pelo modelo são obtidos pelo produto:
>>> Y_est = np.dot(X, B)
>>> Y_est
array([[3264.38629593],
[3725.6400493 ],
[3956.259989 ],
[3889.84426206],
[3759.56562963],
[3106.41116674],
[3068.68275557],
[2878.20102981],
[3051.38134815],
[3884.91244724],
[3182.54558156],
[3830.90297952],
[3324.63158081],
[3584.66737044],
[3901.60967752],
[4625.11081317],
[3475.56739368],
[3367.48158331],
[3941.39804656]])
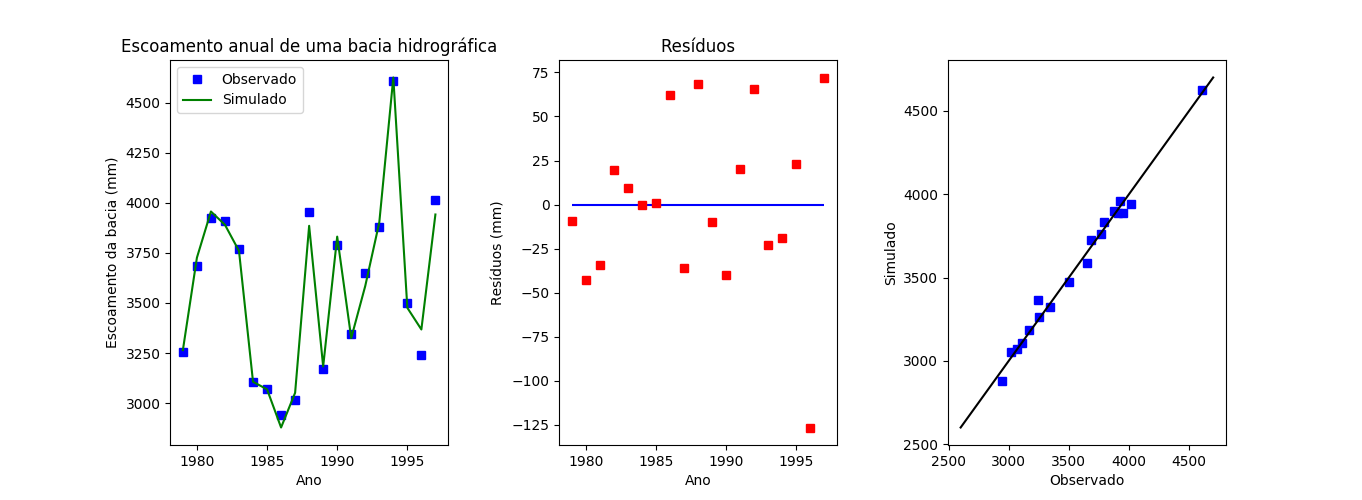
Os gráficos da figura T.5 mostram os valores de escoamento da bacia estimados pelo modelo em relação aos valores de escoamento observados experimentalmente, os resíduos e a correlação entre valores observados e estimados.
Figura T.5. À esquerda o gráfico do escoamento anual da bacia (azul) e os valores simulados pelo modelo (verde). No centro o gráfico dos resíduos (diferença entre os valores observados e os valores simulados). À direita o gráfico a correlação entre os valores observados experimentalmente e os valores simulados.
Os gráficos da figura T.5 foram gerados com os comandos:
#Exibindo os gráficos
#Ajuste do tamanho
plt.figure(figsize=(15,5))
#Cria subplot com separação horizontal
plt.subplot(1,3,1)
#Extraindo os anos T
T = data.values[:,0]
print("T :", T)
plt.plot(T, Y, 's', c='blue', label='Observado')
plt.plot(T, Y_est, '-', c='green', label='Simulado')
plt.xlabel('Ano')
plt.ylabel('Escoamento da bacia (mm)')
plt.title('Escoamento anual de uma bacia hidrográfica')
plt.legend()
plt.subplot(1,3,2)
#Cálculo da matriz dos resíduos E (erros de previsão)
E = Y - Y_est
plt.plot(T, E, 's', c='red')
plt.hlines(y=0, xmin=T[0], xmax=T[-1], color='blue')
plt.xlabel('Ano')
plt.ylabel('Resíduos (mm)')
plt.title('Resíduos')
plt.subplot(1,3,3)
plt.plot(Y, Y_est, 's', c='blue')
x_lim = plt.xlim()
y_lim = plt.ylim()
print(x_lim, y_lim)
#plt.plot(x_lim, y_lim, c='black')
#Gráfico Identidade
plt.plot( [2600, 4700], [2600, 4700], c='black')
plt.xlabel('Observado')
plt.ylabel('Simulado')
#Aumentar espaço entre os gráficos
plt.subplots_adjust(wspace=0.4)
plt.show()
Nota
Os comandos usados nesta seção estão organizados em um único arquivo disponível no link: regressao_multivariada_00.py.