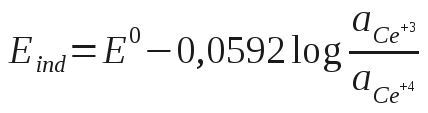Fontes: Skoog, 2002 e Handbook of Chlorination, 2010.
Os métodos potenciométricos de análise estão baseados em medidas do potencial de células eletroquímicas na ausência de correntes apreciáveis. E o equipamento necessário para medidas de potencial inclui:
Eletrodo de referência
Eletrodo indicador
Dispositivo para medida de potencial
O eletrodo de referência ideal tem um potencial que é conhecido, constante, e completamente insensível à composição da solução em estudo.
Na seção D.1.1.1: Potenciais de Eletrodos foi visto o uso do eletrodo de hidrogênio padrão como o eletrodo de referência. Mas o eletrodo de hidrogênio não é prático para medidas rotineiras devido às dificuldades para preparar a superfície do eletrodo e manter as atividades dos reagentes.
Na prática se utilizam eletrodos de referência de fácil preparação e manutenção tais como o eletrodo de prata-cloreto de prata e o de calomelano.
O mais comum é o eletrodo de prata-cloreto de prata o qual pode ser preparado pela aplicação de um potencial oxidante a um fio de prata imerso em solução diluída de ácido clorídrico. Uma fina cobertura de cloreto de prata é formada e adere fortemente ao fio. O fio é, então, imerso em uma solução de cloreto de potássio 3,5M ou saturada. Uma ponte salina conecta a solução de cloreto de potássio ao sistema de eletrodo que está sendo estudado.
Figura D.24. Eletrodos de referência Ag/AgCl (Fonte: www.ufjf.br/nupis/files/2012/04/aula-2-eletroanal%C3%ADtica.pdf)
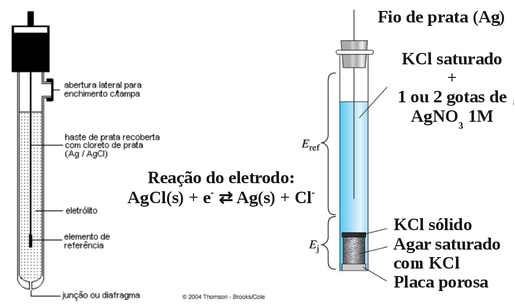
A representação esquemática da célula prata-cloreto de prata é:
Ag | AgCl(sol. sat.), KCl(xM) ||
As linhas verticais simples representam os limites entre as fases (líquida e sólida) através das quais podem surgir diferenças de potencial. Assim uma parte do potencial da célula é a diferença de potencial no limite de fases entre o eletrodo de prata e a solução saturada de AgCl. Pequenas diferenças de potencial também surgem nas junções líquidas, por isso as duas linhas verticais são inseridas entre a solução de KCl e o meio externo.
O potencial do eletrodo de prata-cloreto de prata é determinado pela semi-reação:
Tabela D.1. Potenciais do eletrodo de prata-cloreta de prata (V) X Eletrodo Padrão de Hidrogênio (EPH) em diferentes temperaturas. (Fonte: Skoog, 2002)
| Temperatura (°C) | Ag/AgCl (3,5M) | Ag/AgCl (Saturado) |
|---|---|---|
| 10 | 0,215 | 0,214 |
| 15 | 0,212 | 0,209 |
| 20 | 0,208 | 0,204 |
| 25 | 0,205 | 0,199 |
| 30 | 0,201 | 0,194 |
| 35 | 0,197 | 0,189 |
| 38 | - | 0,184 |
| 40 | 0,193 | - |
Ao usar os eletrodos de referência, como mostra a figura D.24, o nível do líquido interno deve ser mantido sempre acima da solução da amostra para impedir a contaminação da solução do eletrodo e o entupimento da junção devido à reação da solução do analito com os íons prata da solução interna. O entupimento da junção é provavelmente a fonte mais comum de comportamento errático da célula em medidas potenciométricas.
Com o nível do líquido acima da solução no analito, alguma contaminação da amostra é inevitável. Mas na maioria dos casos, a extensão da contaminação é tão pequena que não precisa ser considerada. Mas na determinação de íons como: cloreto, potássio e prata, entretanto, deve-se tomar cuidado para evitar essa fonte de erros.
Um eletrodo indicador ideal tem resposta rápida e reprodutível a variações na atividade do íon que está sendo analisado. Embora nenhum eletrodo indicador seja absolutamente específico na resposta, estão disponíveis alguns com acentuada seletividade. Há dois tipos de eletrodos indicadores: metálico e de membrana.
Os eletrodos indicadores metálicos podem ser classificados em quatro tipos:
Um eletrodo de primeira classe (ou do primeiro tipo) está em equilíbrio direto com o cátion derivado do metal do eletrodo. Por exemplo, um eletrodo indicador de cobre pode ser feito apenas com um fio de cobre (Química Nova - 1984), para o qual se pode escrever a seguinte reacão:
Aplicando a equação de Nernst simplificada (6) e a razão Q (8 - lembrar que a atividade de uma substância pura na fase condensada, sólido ou líquido, é normalmente “1”), pode-se deduzir que o potencial Eind deste eletrodo é dado pela equação:
Equação D.43. Fórmula do potencial do eletrodo indicador de cobre e o gráfico de Eind X pCu (pCu é o logaritmo negativo da atividade do íon Cu+2, aCu+2).
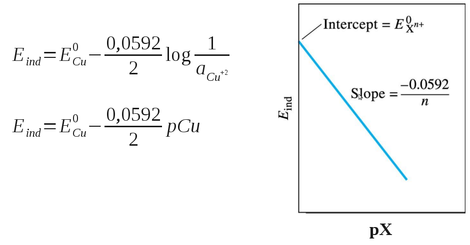
Assim, o eletrodo de cobre fornece uma medida direta de pCu da solução.
No entanto os eletrodos de primeira classe apresentam as seguintes limitações:
Não são muitos seletivos e não respondem somente para os seus cátions, mas também para outros cátions que são mais facilmente reduzidos. Por exemplo, o eletrodo de cobre não pode ser usado na determinação de íons cobre(II) na presença de íons prata(I), que também é reduzido na superfície de cobre.
Alguns eletrodos de primeira classe só podem ser empregados em meio neutro ou básico porque eles se dissolvem na presença de ácidos (Ex: Zn e Cd).
Alguns metais são tão facilmente oxidados que seu uso restringe-se a soluções desaeradas.
Certos metais duros (Fe, Cr, Co e Ni) não apresentam potencial reprodutível.
Responde à atividade de um ânion com o qual o seu íon forme um precipitado ou um complexo estável. Por exemplo, a prata funciona como um eletrodo do segundo tipo para ânions haletos e para ânions que se comportam como haletos.
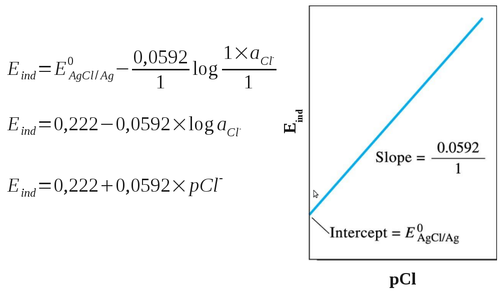
Para preparar um eletrodo para determinar o íon cloreto é necessário formar uma camada de cloreto de prata sobre um eletrodo de prata.
A reação do eletrodo pode ser escrita como:
E a aplicação da equação de Nernst simplificada (6):
Um eletrodo metálico pode, sob determinadas circunstâncias, ser construído para responder a um cátion distinto.
Para mais informações sobre este tipo de eletrodo indicador metálico veja: http://www.ufjf.br/nupis/files/2012/04/aula-2-eletroanal%C3%ADtica.pdf e Skoog, 2002.
Eletrodos de platina, ouro, paládio ou de outros metais inertes servem como eletrodos indicadores para sistemas de oxidação/redução (redox), e são comumente chamados de eletrodos ORP (ORP - Oxidation Reduction Potential). Nessas aplicações, o eletrodo inerte atua como fonte ou depósito para elétrons transferidos de um sistema redox na solução. Por exemplo, o potencial de um eletrodo de platina em uma solução contendo íons Ce(III) e Ce(IV) é dado por:
Assim, um eletrodo de platina pode servir como um eletrodo indicador em uma titulação na qual Ce(IV) atua como reagente padrão.
No entanto, frequentemente, os processos de transferência de elétrons em eletrodos inertes não são reversíveis, e por isso os eletrodos inertes não respondem de maneira previsível a muitas semi-reações encontradas nas tabelas de potenciais de eletrodo.
Por exemplo, um eletrodo de platina em uma solução de tiosulfato e tetrationato não apresenta potenciais reprodutíveis porque o processo de transferência de elétrons:
S4O6-2 + 2e- ⇆ 2S2O3-2
é lento e portanto não é reversível na superfície do eletrodo.
Dentre as diversas técnicas eletroanalíticas, as medidas potenciométricas (ou potenciometria) é a única que está baseada em medidas feitas na ausência de correntes “significativas”.
Inicialmente as técnicas potenciométricas foram utilizadas para a localização do ponto final em titulações (ver também Titration Fundamentals). Mas com o passar do tempo o uso de eletrodos de membrana íon-seletivo passou a permitir a determinação direta da concentração de íons.
A figura D.25 mostra uma célula típica para análise potenciométrica.
Figura D.25. Componentes para medidas de potencial de uma célula galvânica: eletrodo de referência, eletrodo metálico indicador e dispositivo de medida de potencial (potenciômetro). (Fonte: www.ufjf.br/nupis/files/2012/04/aula-2-eletroanal%C3%ADtica.pdf)
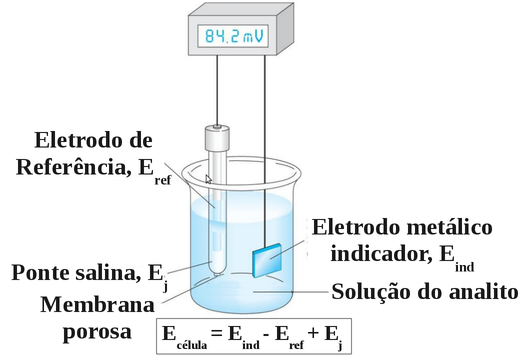
E o potencial da célula (Ecélula), que é obtido experimentalmente, é composto pelos seguintes componentes:
Figura D.26. Componentes que formam o potencial de uma célula potenciométrica (Fonte: www.ufjf.br/nupis/files/2012/04/aula-2-eletroanal%C3%ADtica.pdf)

Segundo a equação:
Ecélula é a diferença de potencial medida pelo instrumento.
O potencial do eletrodo de referência (Eref), em relação ao Eletrodo Padrão de Hidrogênio (EPH), é conhecido e é independente da concentração do analito ou de qualquer outro íon presente na solução.
E o potencial do eletrodo indicador (Eind), em relação ao EPH, depende da atividade do analito e portanto é o que contém a informação analítica, a concentração do analito.
O terceiro componente, o potencial de junção (Ej), é a contribuição da ponte salina que evita a mistura dos componentes da solução com a solução do eletrodo de referência. Esse potencial é gerado pela diferença de mobilidade dos íons da ponte salina. E para minimizar esse potencial utiliza-se um eletrólito que é formado por íons que apresentam mobilidade iônica semelhantes, como o cloreto de potássio (KCl). Na prática o potencial de junção líquida é de alguns milivolts e portanto na maioria dos casos é desprezado.
A determinação potenciométrica compreende as seguintes etapas:
Medir o potencial da célula (Ecélula)
Corrigir o valor medido em função do potencial de referência (Eref) segundo a fórmula D.47
Eind (em relação ao EPH) = Ecélula (medido) - Eref (Ex: Ag/AgCl = 0,222 V)
Calcular a concentração do analito em função do potencial do eletrodo indicador (Eind) com o uso de uma curva de calibração.
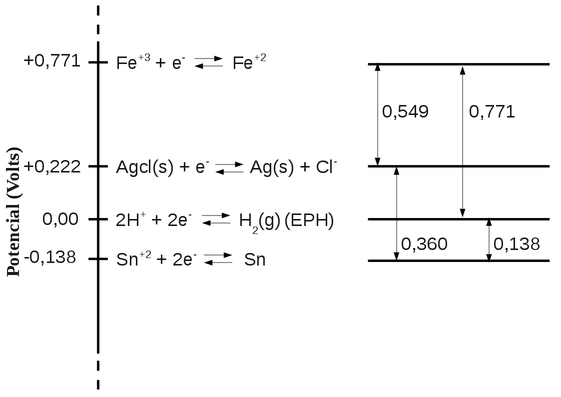
Por exemplo, o potencial de redução do Fe+3 é de +0,771V em relação ao EPH, mas em relação ao eletrodo de referência Ag/AgCl é de 0,549V conforme ilustra o diagrama da figura D.27.
Figura D.27. Diagrama em escada mostrando o potencial de redução do Fe+3 em relação ao Eletrodo Padrão de Hidrogênio (EPH) e ao eletrodo de referência Ag/AgCl. (Fonte: adaptado de Climbing a Potential Ladder to Understanding Concepts in Electrochemistry)