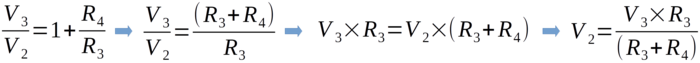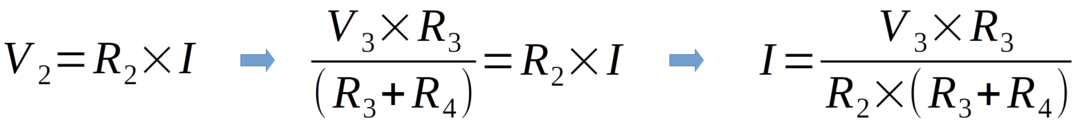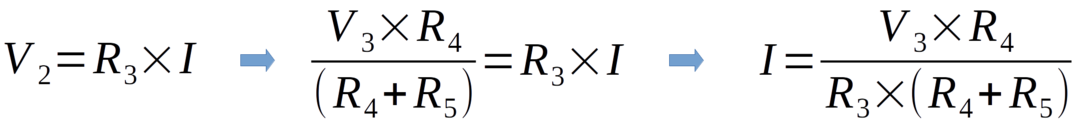Confesso que a procura por informações sobre os métodos de análise de cloro em água tem sido um trabalho incessante e difícil devido às inúmeras alternativas disponíveis, mas também à dificuldade para encontrar orientações “práticas” tais como detalhes sobre os circuitos eletrônicos e os possíveis eletrodos alternativos.
A maior parte das referências mostram apenas gráficos e tabelas com os resultados das leituras obtidas com o uso de instrumentos comerciais, ou somente discussões teóricas.
Dica
Uma fonte com informações práticas sobre montagem e dicas de materiais alternativos é o Journal of Chemical Education.
Podemos organizar os diferentes métodos em 2 grandes grupos: fotométricos e eletroquímicos.
Os métodos fotométricos estão baseados na reação de cloro, e seus derivados, com reagentes “cromogênicos” e posterior quantificação fotométrica.
E os métodos eletroquímicos estão baseados em medidas elétricas (corrente ou potencial) que são correlacionadas direta ou indiretamente, com a concentração de cloro.
Dentre as inúmeras alternativas, priorizei a montagem de um sistema de análise de cloro baseado na “Voltametria”, ou seja, medidas de corrente, em função do potencial, proporcional à concentração do analito.
A vantagem da voltametria é não precisar de reagentes, o que simplifica muito a instrumentação pois dispensa o uso de válvulas e bombas para a dosagem de reagentes.
Uma referência didática para entender as diferentes técnicas para a análise de cloro é o tutorial Continuous Chlorine Detection in Drinking Water and a Review of New Detection Methods.
As técnicas de análise baseadas em medidas de corrente podem ser classificadas em: Voltametria e Amperometria.
Voltametria- Medida de corrente com variação do potencial aplicado.
Amperometria- Medida de corrente com potencial aplicado constante.
A amperometria se baseiam em medidas da corrente elétrica entre três (ou dois) eletrodos mergulhados na amostra. A corrente pode ser gerada espontâneamente nas células “galvânicas” ou induzidas pela aplicação de um potencial nas células “eletrolíticas”.
Na análise amperométrica com aplicação de um potencial externo é necessário o uso de um instrumento chamado de Potenciostato.
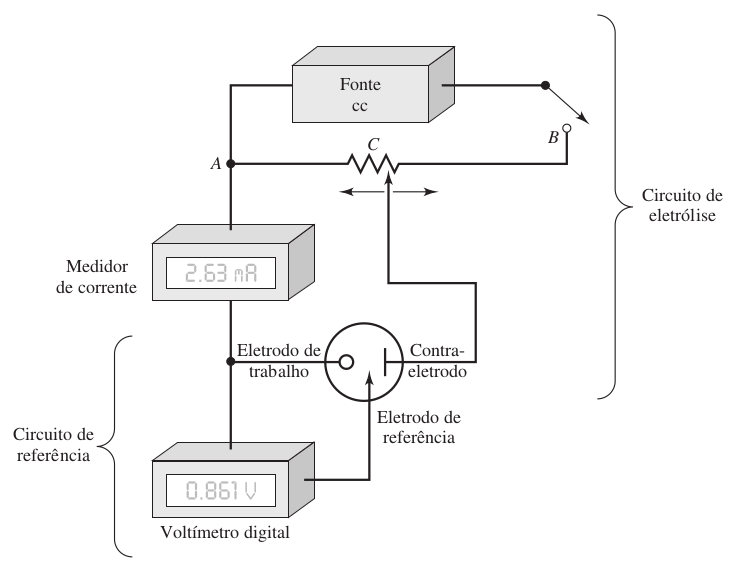
A figura 97 ilustra os elementos conceituais de um potenciostato para uma eletrólise com potencial controlado.
Figura 97. Dispositivo para reações eletrolíticas em potencial catódico (onde ocorre redução) controlado. O contato C é ajustado continuamente para manter o potencial do eletrodo de trabalho sob um potencial constante contra o eletrodo de referência. (Fonte: Skoog, 2002).
Nota
A definição de qual eletrodo é o eletrodo de trabalho (working electrode) e qual é o contra-eletrodo (counter electrode) ou eletrodo auxiliar, é arbitrária. E considera apenas que o eletrodo de trabalho é aquele onde acontece a reação de interesse.
O voltímetro digital monitora o potencial entre o eletrodo de trabalho e o eletrodo de referência. E a tensão aplicada entre o eletrodo de trabalho e o contra-eletrodo (ou eletrodo auxiliar) varia pelo ajuste do contato do potenciômetro em C, para manter o eletrodo de trabalho (neste caso o cátodo) sob um potencial constante em relação ao eletrodo de referência.
Nota
A corrente no eletrodo de referência permanece essencialmente igual a zero durante todo o tempo.
Um instrumento conhecido como potenciostato atua no controle da diferença de potencial entre o eletrodo de trabalho e o contra-eletrodo (ou eletrodo auxiliar) e ajusta essa tensão para manter “sob controle” a diferença de potencial entre o eletrodo de trabalho e o eletrodo de referência como mostra a figura figura 99 (Fonte: Electrochemical Methods: Fundamentals and Applications, 2nd Edition, 2000)
Figura 98. Diagrama esquemático da atuação de um potenciostato em experimentos eletroquímicos com potencial controlado. (Fonte: Electrochemical Methods: Fundamentals and Applications, 2nd Edition, 2000)
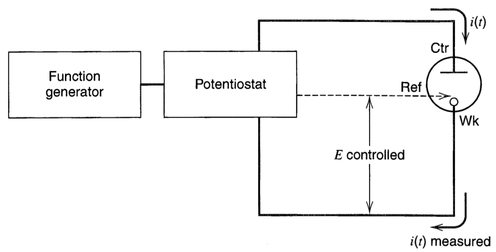
Pode-se ver o potenciostato alternativamente como um elemento ativo cuja função é forçar através do eletrodo de trabalho a corrente necessária para atingir o potencial desejado a qualquer momento. Como a corrente e o potencial estão relacionados funcionalmente, essa corrente é única. Quimicamente, é o fluxo de elétrons necessário para suportar os processos eletroquímicos ativos em taxas compatíveis com o potencial aplicado. Assim, a resposta do potenciostato (corrente) é a resposta experimental mensurável. (Fonte: Electrochemical Methods: Fundamentals and Applications, 2nd Edition, 2000)
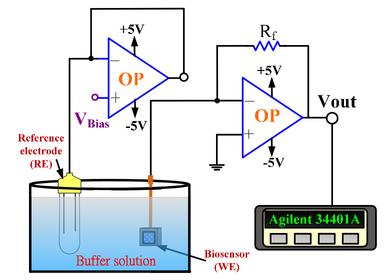
Mas o que se usa na prática são circuitos baseados no uso de Amplificadores Operacionais como mostra a figura 99 correspondente a um potenciostato com “3 ”eletrodos.
Figura 99. Principais componentes de um potenciostato com 3 eletrodos utilizando Amplificadores Operacionais (AO). O AO U2 aplica uma diferença de potencial entre o eletrodo de trabalho (WE) e o eletrodo de referência (RE) que corresponde à diferença: VWE - VRE = -Vref. Ele também impede a passagem de corrente pelo eletrodo de referência (RE). E o AO U1 converte a corrente (Isense) que passa pelo eletrodo de trabalho (WE) em potencial com uma taxa de amplificação proporcional a RT e igual ao produto: RT × Isense. A qual é registrada pelo microcontrolador (μcontroller).(Fonte: Signal conditioning for electrochemical sensors).
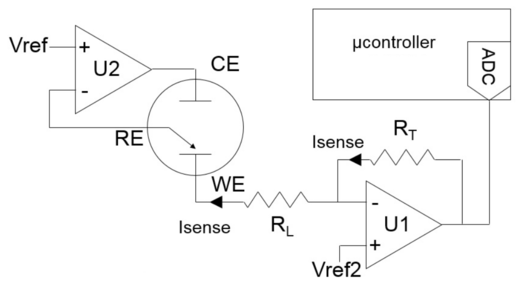
Mas as medidas amperométricas também podem ser feitas com um potenciostato usando apenas “2” eletrodos, sem o eletrodo de referência, como mostra a figura 100.
Figura 100. Principais componentes de um potenciostato com 2 eletrodos utilizando Amplificadores Operacionais (AO). O AO U2 funciona como um seguidor de voltagem e aplica o potencial Vref no contra-eletrodo (CE). E o AO U1 converte a corrente (Isense) que passa pelo eletrodo de trabalho (WE) em potencial com uma taxa de amplificação proporcional a RT e igual ao produto: RT × Isense. A qual é registrada pelo microcontrolador (μcontroller).(Fonte: Signal conditioning for electrochemical sensors).
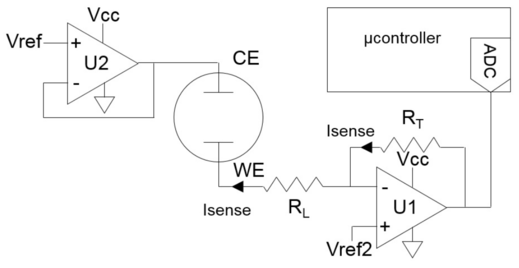
E no artigo Development of Anodic Titania Nanotubes for Application in High Sensitivity Amperometric Glucose and Uric Acid Biosensors encontrei o diagrama bem didático de um potenciostato usando apenas 2 eletrodos como mostra a figura 101.
Figura 101. Diagrama de circuito amperométrico com 2 eletrodos. (Fonte: Development of Anodic Titania Nanotubes for Application in High Sensitivity Amperometric Glucose and Uric Acid Biosensors).
No início, a voltametria era feita com um sistema de dois eletrodos e não com três, como mostrado na figura 99.Com um sistema de dois eletrodos, o segundo eletrodo deve ser um eletrodo metálico grande, como um poço de mercúrio, ou um eletrodo de referência grande o suficiente para impedir sua polarização durante um experimento.
Esse segundo eletrodo combina as funções do eletrodo de referência e do contra-eletrodo. Neste caso, considera-se que o seu potencial permanece constante durante uma varredura de modo que o potencial do eletrodo é simplesmente a diferença entre o potencial aplicado e o potencial do segundo eletrodo.
No entanto, em soluções com alta resistência elétrica, essa hipótese não é válida porque a queda ôhmica (IR) torna-se significativa e aumenta com o aumento da corrente. A consequência são voltamogramas distorcidos.
E por isso, atualmente a maioria dos trabalhos são feitos com três eletrodos. Mas com o objetivo de dispor de um sistema “simples mas útil” resolvi experimentar a montagem de um potenciostato para a determinação voltamétrica, ou amperométrica, de cloro ativo em água.
Nota
Para relembrar:
Voltametria- Medida de corrente com variação do potencial aplicado.
Amperometria- Medida de corrente com potencial aplicado constante.
Uma referência importante foi o artigo Simple Miniaturized Amperometric Flow Cell for Monitoring Residual Chlorine in Tap Water que mostra o uso da técnica de amperometria com uma cela de fluxo com apenas 2 eletrodos, um eletrodo de platina e um eletrodo de Ag/AgCl.
Mas a principal proposta deste site é documentar soluções simples e acessíveis utilizando sucata e materiais de uso cotidiano. E portanto comecei a pensar em materiais alternativos para substituir os materiais convencionais.
Para substituir a platina resolvi experimentar o filamento de resistência de chuveiro como na figura 102.
Desenrolei um pedaço da espiral e cortei um segmento de ~15cm. Escolhi esse material considerando que deveria ser uma liga com alguma estabilidade eletroquímica para permanecer em água e não oxidar com facilidade dentro do chuveiro.
O Prof. Gary Mabbott fez os seguintes comentários sobre o uso desse material como eletrodo:
In the US, heating elements like the one you have described are made with nichrome wire. That is an alloy that is 80% Ni and 20% Cr. I have never used nichrome or seen it described as a material for a working electrode in the literature. However, one of the advantages of being new to a particular field is that you may have an idea that more experienced people would not think of. My first thought was that chromium does not transfer electrons easily. Atleast, that is what I thought was the explanation for chromium giving corrosion resistance to steel. But “theory guides, experiment decides.” Try it!
Além disso considerando que o potencial de redução do Fe+2/Fe é de -0,440V (Wikipedia):
Fe+2 + 2e- ⇆ Fe (Eθ = -0,440)
Imaginei que esse material poderia suportar potenciais de, pelo menos, até 0,440V no caso de ser usado como ânodo em uma célula eletroquímica. O que está abaixo dos 0,5V que foi estudado no artigo Simple Miniaturized Amperometric Flow Cell for Monitoring Residual Chlorine in Tap Water
E como alternativa a um filamento de prata (Ag) recoberto com cloreto de prata (AgCl), experimentei recortar um pedaço da membrana de plástico com trilhas condutivas utilizadas em alguns teclados como mostra a figura 103.
Figura 103. Membrana de teclado com trilhas de prata usada para montar um eletrodo de referência Ag/AgCl, com destaque do pedaço de membrana e o suporte de acrílico para fixação.

Em alguns teclados essas trilhas condutivas são feitas de prata (Wikipedia) e basta limpar com uma borracha para melhorar a condutividade.
A membrana com as trilhas de prata foi colocada por 10 minutos em solução concentrada de hipoclorito (água sanitária) para gerar uma camada superficial de AgCl. E o eletrodo metálico da resistência de chuveiro foi colocado dentro de uma seringa de insulina com o septo perfurado para manter apenas alguns milímetros da extremidade do fio em contato com a solução como mostra a figura 104.
Figura 104. À esquerda a trilha de prata em solução concentrada de hipoclorito de sódio para a formação de uma camada de AgCl. E à direita o filamento de resistência de chuveiro dentro de uma seringa de insulina e a extremidade exposta para contato com a solução.

Como não é possível fazer solda na folha de plástico, recortei o pedaço de uma chapa de circuito impresso, lixei para remover a tinta e expor a chapa de cobre, e fixei sobre a membrana com um prendedor de papel como mostra a figura 105.
Figura 105. Montagem dos eletrodos usados nos testes com o potenciostato. Á direita uma imagem ampliada do eletrodo de Ag/AgCl e o eletrodo metálico de resistência de chuveiro.

Os testes foram feitos com um circuito montado em protoboard, AO LM358N, e leituras feitas com o monitor serial da IDE do Arduino como descrito na próxima seção.
Precisamos gerar um potencial que será aplicado ao eletrodo a um dos eletrodos enquanto o outro eletrodo permanece no terra (gnd).
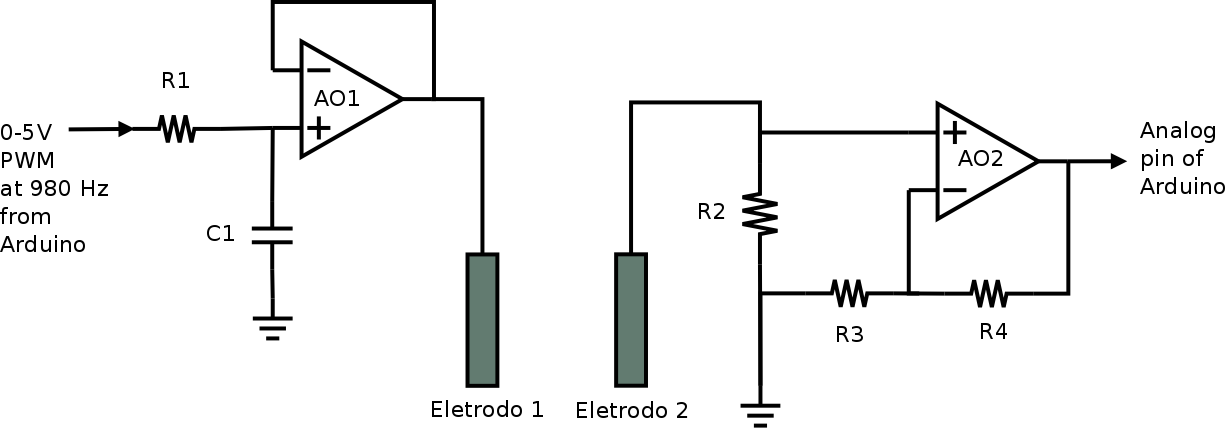
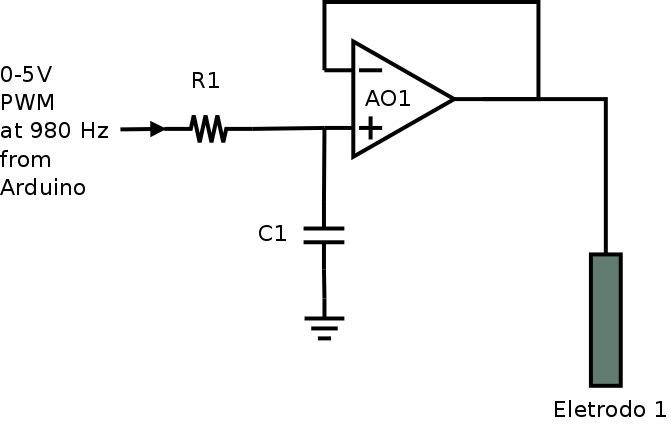
Para isso vamos usar o sinal PWM gerado por um pino digital do Arduino e transformar em um sinal com potencial “constante” (ou quase constante) utilizando um filtro RC como mostra a figura 106.
Figura 106. Circuito com filtro RC na entrada não inversora de um AO (AO1) configurado como um seguidor de voltagem.
Para avaliar os valores mais adequados para R1 e C1 podemos usar o simulador disponível no site RC Low-pass Filter Design for PWM.
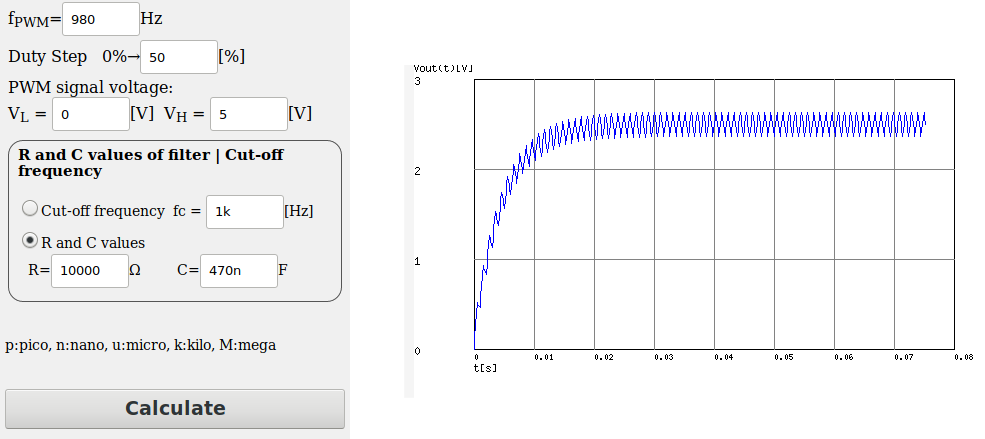
Usando os valores indicados no artigo Building a Microcontroller Based Potentiostat: A Inexpensive and Versatile Platform for Teaching Electrochemistry and Instrumentation obtemos a simulação como na figura 107.
Figura 107. Simulação do sinal de saída para o filtro RC com R=10kΩ, C=470nF, frequência do pulso PWM= 980Hz e amplitude do sinal de 0-5V, largura de pulso (duty cycle) = 50%.
Nota
O Arduino UNO gera pulsos PWM nos pinos digitais com frequência de 480Hz, mas nos pinos 5 e 6 a frequência de PWM é 980Hz. (Ver: analogWrite())
Mas também existe a seguinte nota:
The PWM outputs generated on pins 5 and 6 will have higher-than-expected duty cycles. This is because of interactions with the millis() and delay() functions, which share the same internal timer used to generate those PWM outputs. This will be noticed mostly on low duty-cycle settings (e.g. 0 - 10) and may result in a value of 0 not fully turning off the output on pins 5 and 6.
A maior parte dos projetos de potenciostatos usa um amplificador operacional (AO) no modo amplificador inversor como conversor I-V (amplificador de transimpedância). E a tensão na saída do AO é lida pelo pino analógico do Arduino para medir a corrente que circula entre os eletrodos (de trabalho e auxiliar).
Mas isso exige o uso de uma fonte simétrica para permitir aplicar sinais positivos e negativos entre os eletrodos. Além disso também é necessário implementar um conversor de sinal bipolar para unipolar pois o Arduino não é capaz de ler sinais negativos no pino analógico.
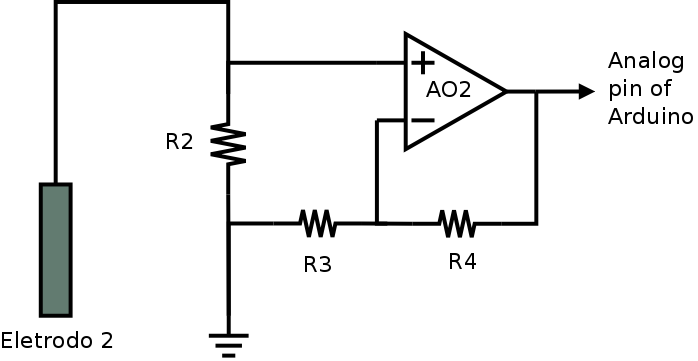
Para tentar simplificar o circuito e usar uma fonte simples resolvi experimentar o uso de um AO no modo amplificador não-inversor para fazer a leitura de corrente entre os eletrodos conforme a figura 108.
Figura 108. Módulo para a conversão da corrente em tensão usando um AO (AO2) configurado como um amplificador não-inversor.
Veja a simulação desse circuito no link Noninverting Amplifier para entender o funcionamento desse módulo.
A figura 109 mostra o circuito completo com os dois eletrodos.
Vamos agora selecionar os melhores valores de R1 e C1 no circuito 106, para gerar uma saída analógica com mínima ondulação possível. (Ver:DAC com sinal PWM)
Para fazer os testes iniciais vamos programar o Arduino para gerar um sinal PWM com diferentes larguras de pulso.
Iniciamos um código simples apenas para gerar o sinal PWM e fazer uma leitura pelo osciloscópio, como mostra a figura 110
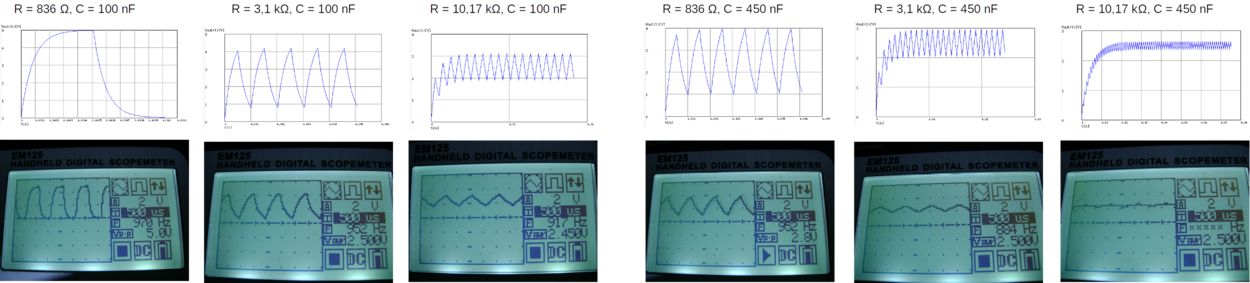
Montamos na protoboard o filtro RC com uma resistência variável, dois capacitores (100 nF e 450 nF) e fizemos simulações e medidas com um osciloscópio como mostra a figura 111
Dica
Para quem quiser conhecer o funcionamento deste osciloscópio veja os tutoriais Scopemeter EM125 #1, Scopemeter EM125 #2 e o manual.
Como se pode observar na figura 111 a combinação de R = 10,17kΩ e C = 450 nF produziu o sinal analógico mais estável. Aumentamos a resistência para 20 kΩ e o sinal analógico melhorou um pouco mais.
Em seguida estudamos a aplicação do sinal na entrada não-inversora de um aplificador operacional configurado como seguidor de voltagem e utilizamos o amplificador LM358N como mostra a figura 112.
Figura 112. Circuito com filtro RC na entrada não inversora do AO LM358N, alimentado por uma “Fonte Simples” (Single Supply ou Unipolar - 0/Vcc) e configurado como um seguidor de voltagem.
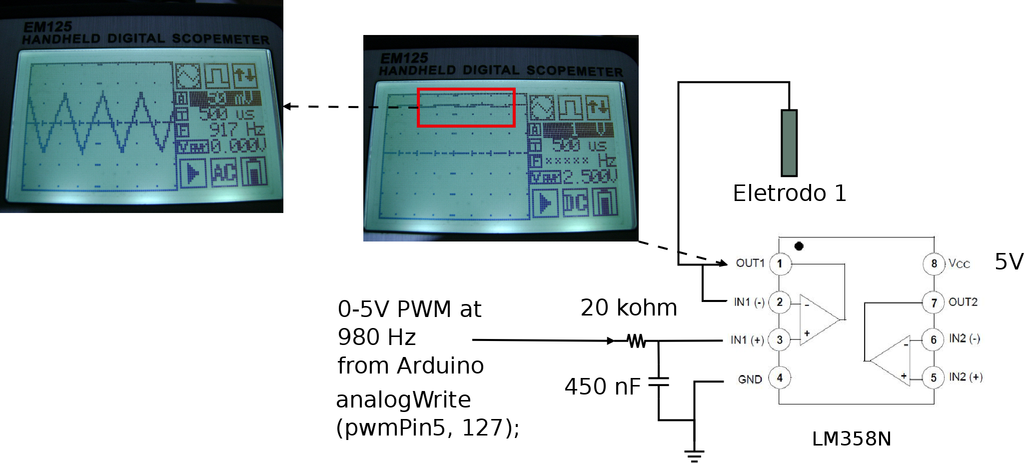
As leituras no osciloscópio mostram que o sinal PWM produzido pelo Arduino com largura de pulso de 50%, produzido pelo comando analogWrite(pwmPin5, 127);, é transformado pelo filtro RC em um sinal com valor médio de 2,5V e oscilação de ±50 mV (2,45 - 2,55 V).
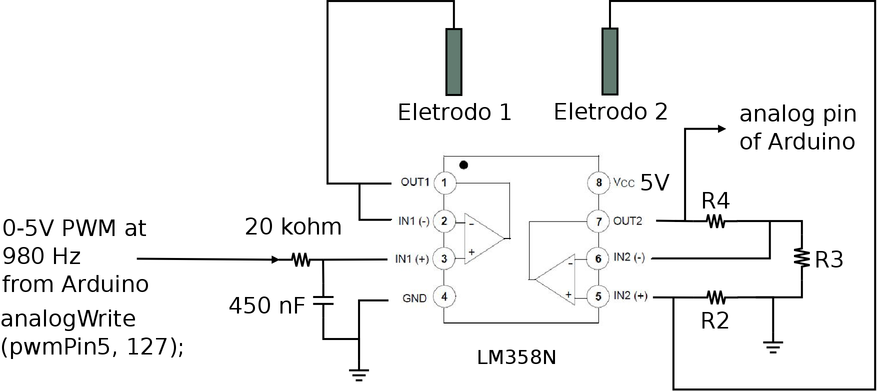
Em seguida passamos à montagem da segunda parte do circuito utilizando o segundo AO do LM358N na configuração de um amplificador não-inversor para fazer a leitura de corrente que circula pelo eletrodo 2 como mostra a figura 113.
Para avaliar o comportamento do circuito vamos fazer experimentos de “polarização de resistores”, ou seja, substituir os eletrodos por um resistor de valor conhecido como mostra a figura 114.
Figura 114. Avaliação do funcionamento do potenciostato usando um resistor (Rm), de valor conhecido, no lugar dos eletrodos em solução.
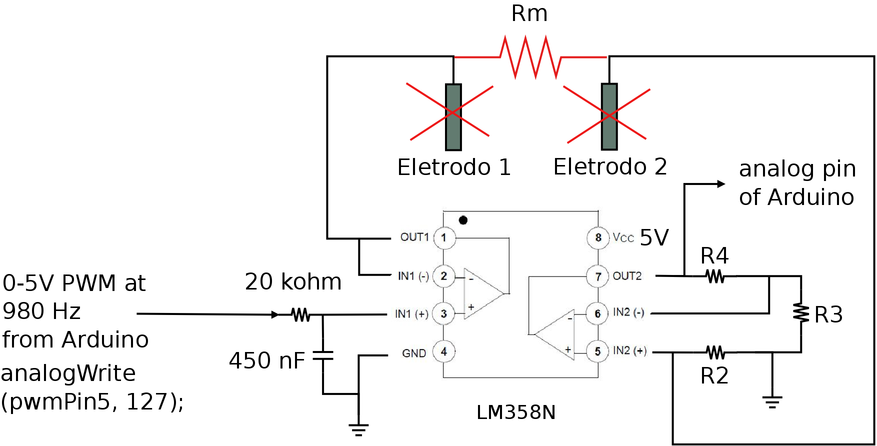
Implementamos inicialmente o seguinte código na placa Arduino para aplicar diferentes potenciais em Rm e medir a corrente que passa através de R2.
/*
Code to control a tiny potentiostat
*/
const byte analog_input_0 = A0; // analog pin
const byte pwm_output_5 = 5; // digital pin 5 for pwm output at 980Hz
byte pwm;
float vi; //voltage applied
float vo; //output voltage
void setup() {
Serial.begin(9600);
Serial.flush();
pinMode(pwm_output_5, OUTPUT); // sets the pin as output
}
void loop() {
Serial.println("Start scan");
Serial.println("Tensão aplicada(V);Tensão lida (V)");
//Start de foward scan
for (pwm = 0; pwm <= 127; pwm++){
analogWrite(pwm_output_5, pwm);
vi = pwm * 5.0 / 255.0;
Serial.print(vi);
Serial.print(";");
delay(200);
vo = analogRead(analog_input_0) * 5.0 / 1023.0;
Serial.println(vo);
}
//pwm is byte type so avoid compare pwm>=0
//because if pwm = 0 the pwm--
//will convert pwm to 255!
for (pwm = 127; pwm > 0; pwm--) {
analogWrite(pwm_output_5, pwm);
vi = pwm * 5.0 / 255.0;
Serial.print(vi);
Serial.print(";");
delay(200);
vo = analogRead(analog_input_0) * 5.0 / 1023.0;
Serial.println(vo);
}
Serial.println("End scan");
delay(10000);
}
O sinal PWM foi gerado pelo pino 5 e a tensão na saída do pino 7 do LM358N foi ligada no pino analógico A0 do Arduino.
A saída PWM do Arduino corresponde a uma sequência de ondas quadradas no intervalo de 0-5V, mas nos processos eletroquímicos em água não se trabalha “usualmente” com diferenças de potencial maiores do que 1,5V pois o objetivo é oxidar ou reduzir as espécies dissolvidas em água mas sem oxidar ou reduzir o próprio solvente (água). Esse intervalo é conhecido por janela eletroquímica (Ver também: janela de estabilidade eletroquímica).
Por isso o programa gera pulsos PWM até 127, o que gera um sinal de ~2,5 V, ou seja, metade da largura de pulso máxima (255 -> 5V).
Entendendo as correntes!
O potencial positivo aplicado pelo pino 1 do LM358N irá gerar um fluxo de corrente através de Rm e R2. O ponto intermediário entre Rm e R2 está ligado ao pino 5 do LM358 que corresponde à entrada não-invesora do AO.
A entrada não inversora de um AO possui uma impedância alta mas não “infinita” e portanto parte da corrente que sai de Rm deve estar sendo drenada pela entrada não-inversora do AO (pino 5).
O objetivo é ter uma “estimativa” da corrente que circula pela cela eletrolítica (em mA) a partir da tensão amplificada na saída do AO.
Por isso Determinamos uma equação de calibração que correlaciona a corrente que passa por R2 com a tensão amplificada (Vo) lida pela placa Arduino.
Teoricamente o ganho (amplificação), considerando a cofiguração atual (R3 = 957 Ω e R4 = 98300 Ω) é dado pela fórmula:
(R3 + R4) / R3 = (957 + 98300)/957 = 103,7
Para fazer essa calibração utilizamos uma resistência (Rm) com o valor de Rm = 9820 Ω e R2 = 98 Ω. A corrente que passa por essas duas resistências em séria é calculada pelo Lei de Ohm (desconsiderando as perdas pela entrada não inversora do AO - pino 5).
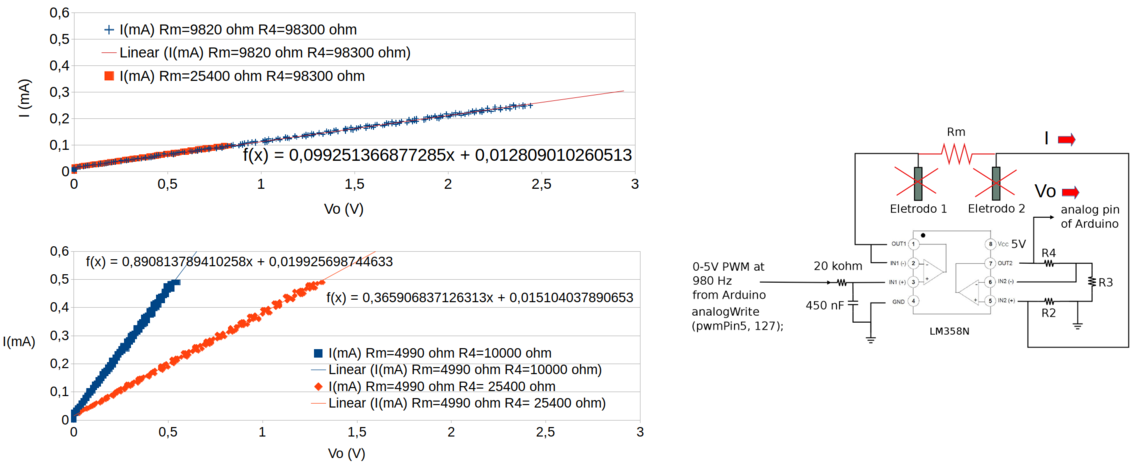
Os resultados dessas medidas apresentaram boa linearidade conforme o gráfico da figura 115.
Figura 115. Gráfico da correlação entre a corrente (mA) e a tensão amplificada (Vo) na saída do AO (pino 7 do AO). Considerando o circuito da figura 114, com Rm = 9820 Ω, R2 = 98 Ω, R3 = 957 Ω e R4 = 98300 Ω.
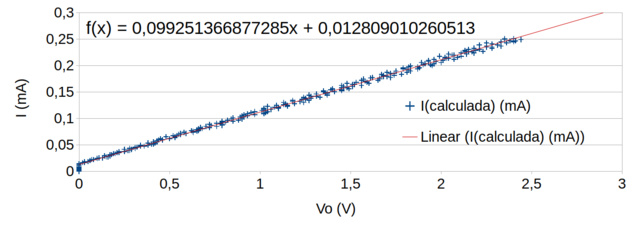
Para termos uma percepção mais detalhada do comportamento do circuito para diferentes valores de corrente decidimos fazer mais uma varredura com Rm = 25400 Ω, e os resultados estão incluídos no gráfico da figura 116.
Figura 116. Gráfico da correlação entre a corrente (mA) e a tensão amplificada (Vo) na saída do AO (pino 7 do AO) para 2 valores de Rm (9820 Ω e 25400 Ω).
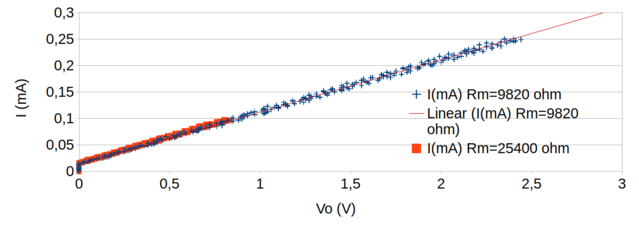
Para determinar a corrente que circula pelos eletrodos (I) a partir do potencial amplificado (Vo) podemos usar diferentes equações de calibração dependendo do ganho do amplificador.
I(mA) = 0,09925 × Vo(V) + 0,01281
Configuração: R2 = 98 Ω, R3 = 957 Ω e R4 = 98300 Ω.
I(mA) = 0,3659 × Vo(V) + 0,0151
Configuração: R2 = 98 Ω, R3 = 957 Ω e R4 = 25400 Ω.
I(mA) = 0,8908 × Vo(V) + 0,01992
Configuração: R2 = 98 Ω, R3 = 957 Ω e R4 = 10000 Ω.
A figura 117 mostra os gráficos correspondentes.
Figura 117. Gráfico da correlação entre a corrente (mA) e a tensão amplificada (Vo) na saída do AO (pino 7 do AO) para diferentes configurações.
O código inicial implementado na placa Arduino foi melhorado para permitir maior interação e a execução de varreduras (scan) sob demanda.
O objetivo foi incluir funções como start_scan para dar início a uma varredura de potencial apenas quando necessário.
Para uma varredura de potencial (voltametria) é necessário especificar a faixa de potencial (Vinicial - Vfinal) e a velocidade de varredura (mV/s).
Para permitir essa configuração dinâmica podemos implementar no código da placa Arduino funções que permitam interpretar comandos com a estrutura: [comando];[argumento] ou [comando];[argumento_1];[argumento_2].
Exemplos de comandos:
START_SCAN;scan_rate - dá início a uma varredura com velocidade definida por scan_rate usando a unidade mV/s.
SET_RANGE_VOLTAGE;0.0;2.0 - define os limites de potencial usados em uma varredura.
Os comandos START_SCAN e SET_RANGE_VOLTAGE podem ser digitados em letra maiúscula ou minúscula.
Os limites do comando SET_RANGE_VOLTAGE pode ser um “número decimal” representando os limites de potencial em Volt (V).
O parâmetro scan_rate (velocidade de varredura) pode ser um “número decimal” expresso em “mV/s” (Ex: 50 mV/s, 100mV/s, 200mV/s ...). Esse valor deve ser convertido pelo programa em um intervalo de tempo, em milisegundos (ms), entre cada incremento do sinal PWM gerado pelo pino digital da placa Arduino.
Vamos lembrar que a largura do pulso PWM possui uma faixa de 0 a 255 gerando sinais de 0 a 5V (5000 mV) respectivamente. Isso significa que cada unidade da escala PWM corresponde a uma variação de potencial (mínima) de 19,61 mV (5000 mV / 255).
A “velocidade de varredura” (scan_rate) é a variação do potencial (mV) pelo intervalo de tempo:
scan_rate = ΔV(mV) / ΔT(s)
Podemos calcular o intervalo de tempo para cada variação na unidade mínima de potencial (19,61 mV) dividindo ΔT por scan_rate:
ΔT(s) = ΔV(mV) / scan_rate
Por exemplo, para um scan_rate de 100mV/s o intervalo entre cada incremento de PWM deve ser:
scan_rate = ΔV(mV) / ΔT(s)
100 (mV/s) = 19,61(mV) / ΔT(s)
ΔT(s) = 19,61(mV) / 100(mV/s)
ΔT(s) = 0,1961(s)
O intervalo entre cada incremento em PWM deve ser de 0,1961 s ou 196,1 ms, arredondado para 196 ms.
A fórmula de cálculo do intervalo de tempo a partir do scan_rate é:
interval(ms) = ( (5000/255) / scan_rate(mV/s) ) × 1000
Com essas modificações o código para o Arduino passou a ser:
/*
24/02/2021
Code to control a tiny potentiostat
Adapted from:
Example of processing incoming serial data without blocking.
Author: Nick Gammon
(http://www.gammon.com.au/forum/?id=11425)
*/
//Available pins
//Digital
//D2, D3 (PWM), D4, D5(PWM), D6(PWM), D7, D8, D9(PWM), D10(PWM), D11(PWM) e D12
//Analogic
//A0, A1, A2, A3, A4 e A5
const unsigned int MAX_INPUT = 40;
char message[MAX_INPUT];
char *cmd;
char *scan_rate;
char *min_volt;
char *max_volt;
//Max voltage applied by RC filter in mV
const int max_pwm_volt = 5000;
//Default minimum voltage of scan
float e_min = 0.0;
//Default maximum voltage of scan
float e_max = 2.0;
const byte analog_input_0 = A0; // analog pin
const byte pwm_output_5 = 5; // digital pin 5 for pwm output at 980Hz
int pwm;
float vi; //voltage applied
float vo; //output voltage
void setup() {
Serial.begin(9600);
Serial.flush();
pinMode(pwm_output_5, OUTPUT); // sets the pin as output
}
//process_data to process incoming serial data after a terminator received
void process_data (char *data) {
cmd = strtok(data, ";");
if ( (strcmp(cmd, "START_SCAN") == 0) || (strcmp(cmd, "start_scan") == 0) ) {
scan_rate = strtok(NULL, ";");
startScan(scan_rate);
} else if (strcmp(cmd, "SET_RANGE_VOLTAGE") == 0 || strcmp(cmd, "set_range_voltage") == 0) {
min_volt = strtok(NULL, ";");
max_volt = strtok(NULL, ";");
setRangeVoltage(min_volt, max_volt);
} else {
Serial.print("unknown command: ");
Serial.println(cmd);
} // end of if
} // end of process_data
void startScan(char *scan_rate) {
float mV_s = atof(scan_rate);
Serial.print("scan_rate (mV/s): ");
Serial.println(mV_s);
//Interval for each increment in PWM
int interval = (int) ( ( ( ( max_pwm_volt / 255.0 ) / mV_s ) * 1000 ) + 0.5 );
Serial.print("interval (ms): ");
Serial.println(interval);
Serial.print("Range of voltage: ");
Serial.print(e_min);
Serial.print(" - ");
Serial.println(e_max);
Serial.println("Start scan");
Serial.println("Tensão aplicada(Vi);Tensão lida (Vo)");
//Start de foward scan
//https://forum.arduino.cc/index.php?topic=594161.0
//int rounded_integer = (int)(float_number+0.5);
int pwm_min = (int)((e_min * 255.0 / 5.0) + 0.5);
int pwm_max = (int)((e_max * 255.0 / 5.0) + 0.5);
for (pwm = pwm_min; pwm <= pwm_max; pwm++){
analogWrite(pwm_output_5, pwm);
vi = pwm * 5.0 / 255.0;
Serial.print(vi);
Serial.print(";");
delay(interval);
vo = analogRead(analog_input_0) * 5.0 / 1023.0;
Serial.println(vo);
}
//pwm is byte type so avoid compare pwm>=0
//because if pwm = 0 the pwm--
//will convert pwm to 255!
for (pwm = pwm_max; pwm >= pwm_min; pwm--) {
analogWrite(pwm_output_5, pwm);
vi = pwm * 5.0 / 255.0;
Serial.print(vi);
Serial.print(";");
delay(interval);
vo = analogRead(analog_input_0) * 5.0 / 1023.0;
Serial.println(vo);
}
Serial.println("End scan");
analogWrite(pwm_output_5, 0);
}
void setRangeVoltage(char *min_volt, char *max_volt) {
e_min = atof(min_volt);
e_max = atof(max_volt);
int pwm_min = (int)((e_min * 255.0 / 5.0) + 0.5);
int pwm_max = (int)((e_max * 255.0 / 5.0) + 0.5);
Serial.print("Range of voltage: ");
Serial.print(e_min);
Serial.print(" pwm ");
Serial.print(pwm_min);
Serial.print(" - ");
Serial.print(e_max);
Serial.print(" pwm ");
Serial.println(pwm_max);
}
void processIncomingByte (const byte inByte) {
static char input_line[MAX_INPUT];
static unsigned int input_pos = 0;
switch (inByte)
{
case '\n': // end of text
input_line[input_pos] = 0; // terminating null byte
// terminator reached! process input_line here ...
process_data (input_line);
// reset buffer for next time
input_pos = 0;
break;
case '\r': // discard carriage return
break;
default:
// keep adding if not full ... allow for terminating null byte
if (input_pos < (MAX_INPUT - 1))
input_line[input_pos++] = inByte;
break;
} // end of switch
}// end of processIncomingByte
void loop() {
// if serial data available, process it
while (Serial.available () > 0)
processIncomingByte (Serial.read());
// do other stuff here like testing digital input (button presses) ...
}
Lembrar que durante a medida amperométrica de cloro livre o eletrodo de trabalho deve estar com menor potencial para funcionar como cátodo e reduzir o hipoclorito presente. O par redox correspondente será a oxidação da prata no eletrodo de Ag/AgCl que irá funcionar como ânodo.
Mas se for feita uma inversão de polaridade e o eletrodo metálico estiver em maior potencial do que o eletrodo de Ag/AgCl devemos considerar a possibilidade de ocorrer a oxidação do Fe para Fe+2, ou oxidação da água gerando O2 ou a oxidação do cloreto regenerando hipoclorito, dependendo da diferença de potencial aplicado. (Ver:Water electrolysis - what is happening to an iron anode?
A resistência de feedback do conversor I-V (amplificador de transimpedância) deve ser maior do que a resistência interna da solução para que o sinal seja amplificado. Mas se a resistência de feedback for muito alta, a corrente para a reação eletrolítica será baixa.
Se for necessário fornecer mais corrente para a reação de eletrólise o conversor I-V poderia ser substituído por um amplificar diferencial (Ver: Potentiostatic Circuit)
Soluções de Hipoclorito para Testes do Potenciostato
Cálculo da concentração de Cl2 ativo na água sanitária.
Preparamos soluções diluídas de Água Sanitária com teor de cloro ativo na faixa de 1,75 a 2,75% (p/p) (http://www.inmetro.gov.br/consumidor/produtos/agua_sanitaria2.asp e Águas sanitárias no mercado brasileiro) para avaliar a sensibilidade dos métodos estudados.
Como um valor “nominal aproximado” de referência vou considerar uma concentração média de 2,25% (p/p), isso significa 2,25g de Cl2/100g de solução ≅ 22,5g Cl2/1L de solução (considerando a densidade da solução ≅ 1 Kg/L).
Ou seja, a água sanitária tem uma concentração média estimada em cloro ativo de 22500 mgCl2/L ou 22500 ppm.
Nota
Conforme a portaria no. 2.914/2011 o responsável pelo sistema de abastecimento deve assegurar que a água fornecida contenha um teor mínimo de cloro residual livre de 0,5 mg/L. Mas é “obrigatório” que as concentrações de cloro residual livre em qualquer ponto do sistema de abastecimento seja de no “mínimo” 0,2 mg/L (ou 2 mg/L de cloro residual combinado), e no “máximo” de 2 mg/L.
E como solvente para as diluições, seguimos o artigo Simple Miniaturized Amperometric Flow Cell for Monitoring Residual Chlorine in Tap Water e preparamos uma solução a 200 mg/L (200 ppm) de NaCl dissolvendo 0,2g NaCl em 1L de água (3,4×10-3 M).
Tabela 13. Soluções de Cloro Livre para testes com o potenciostato.
| Número da solução | mgCl2/L |
|---|---|
| 0 | 0 |
| 1 | 0,69 |
| 2 | 5,5 |
| 3 | 43,9 |
| 4 | 351,6 |
| 5 | 2812,5 |
Fizemos os primeiros testes com todas as soluções e foi possível observar um sinal no intervalo de 0,6V até ~1,5V. Mas as leituras apresentaram muita oscilação. Então escolhi apenas a solução 4 para fazer os primeiros testes exploratórios e entender o funcionamento do instrumento.
Selecionamos a solução 4 (351,6 ppm Cl2 livre) e foram feitas varreduras com diferentes velocidades: 50mV/s, 100mV/s, 200mV/s e 400mV/s. A figura 118 mostra os gráficos correspondentes.
Figura 118. Na parte superior o gráfico com as leituras de potencial na saída do AO (Vo) em função do potencial aplicado (Vi) para diferentes velocidades de varredura. E na parte inferior apenas as varreduras com 50mV/s e 400mV/s
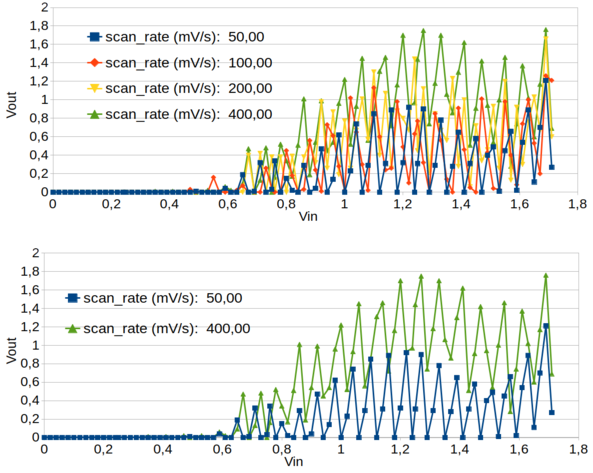
Pode-se notar que com o aumento da velocidade de varredura as leituras de Vo tendem a se distanciar do valor 0 no intervalo entre 0,6V até ~1,5V. Mas ainda persiste a grande oscilação das leituras.
Não sabia se essa oscilação das leituras era uma oscilação inerente aos processos eletroquímicos de oxidação e redução ou se era apenas um efeito de subamostragem das leituras feitas pelo Arduino. Então resolvi estudar o efeito do aumento na taxa de amostragem.
Aumentei para 3 leituras de Vo em cada patamar de tensão mas não houve melhora como mostra a figura 119.
Figura 119. Na parte superior o gráfico com 3 leituras de potencial na saída do AO (Vo) em função do potencial aplicado (Vi) apenas na varredura direta. E na parte inferior apenas o valor médio.
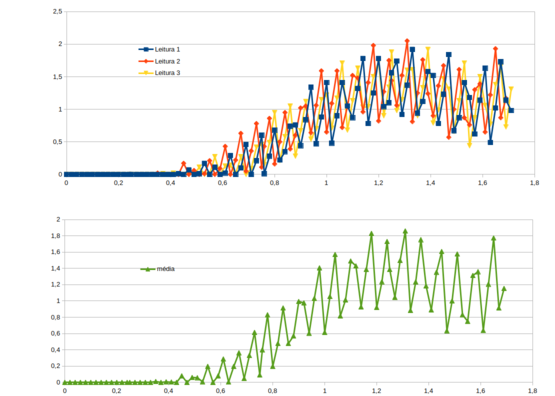
Aumentei para 10 leituras em cada patamar e pude observar uma melhora no sinal como mostra a figura 120.
Figura 120. Gráfico com a média de 10 leituras de potencial na saída do AO (Vo) na varredura, direta e reversa, da solução 4 com velocidade de 400mV/s.
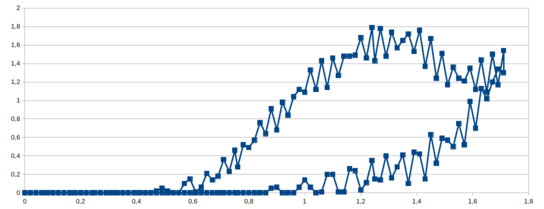
E a figura 121 mostra o resultado com “50” leituras em cada patamar.
Figura 121. Gráfico com a média de 50 leituras de potencial na saída do AO (Vo) na varredura, direta e reversa, da solução 4 com velocidade de 400mV/s.
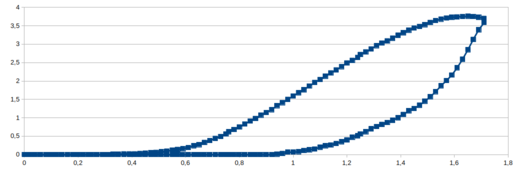
Para aumentar a taxa de amostragem foi incluído os seguintes comandos no código do Arduino:
average_vo = 0;
for (int i=0; i > 50; i++) {
average_vo = average_vo + (analogRead(analog_input_0) * 5.0 / 1023.0);
delay(interval/50);
}
average_vo = average_vo/50.0;
Com a melhora no sinal foi possível fazer a varredura direta e reversa de todas as soluções com velocidade de varredura de 400 mV/s como mostra a figura 121 mostra o resultado com “50” leituras em cada patamar.
Figura 122. Gráfico com varredura direta e reversa de todas as soluções, usando a média de 50 leituras de potencial na saída do AO (Vo) com velocidade de 400mV/s.
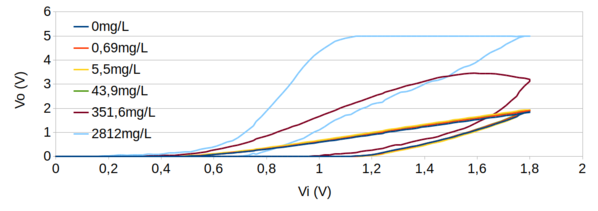
O objetivo deste teste era avaliar a sensibilidade da atual configuração do potenciostato (R2=197Ω R3=957Ω e R4=98000Ω) para uma ampla faixa de concentração de Cloro Livre. Pode-se observar que o sistema foi capaz de identificar variação no sinal a partir da região de 351 mgCl2/L. Mas a concentração de 2812,5 mgCl2/L ficou acima da escala de leitura (>5V).
A partir de agora vamos avaliar modificações no circuito para tentar aumentar a sensibilidade do potenciostato para baixas concentrações de Cloro Livre.
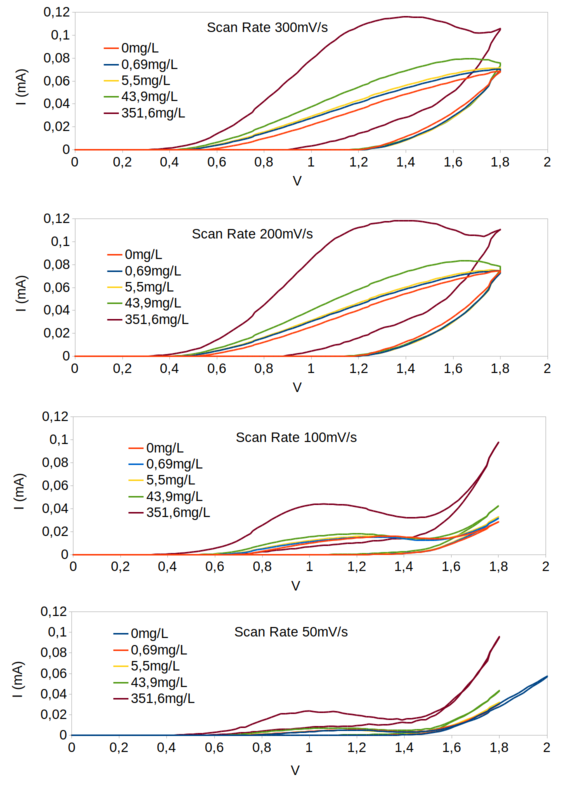
Para melhorar o ganho do AO substituímos R4 por um resistor de 198.000Ω (Configuração: R2=197Ω R3=957Ω e R4=198.000Ω), e fizemos uma nova série de medidas com as soluções 0-4 com diferentes velocidades de varredura (scan_rate): 50, 100, 200 e 300 mV/s como mostra a figura 123.
Usamos como critério para o cálculo da corrente a equação do amplificador não-inversor e a Lei de Ohm.
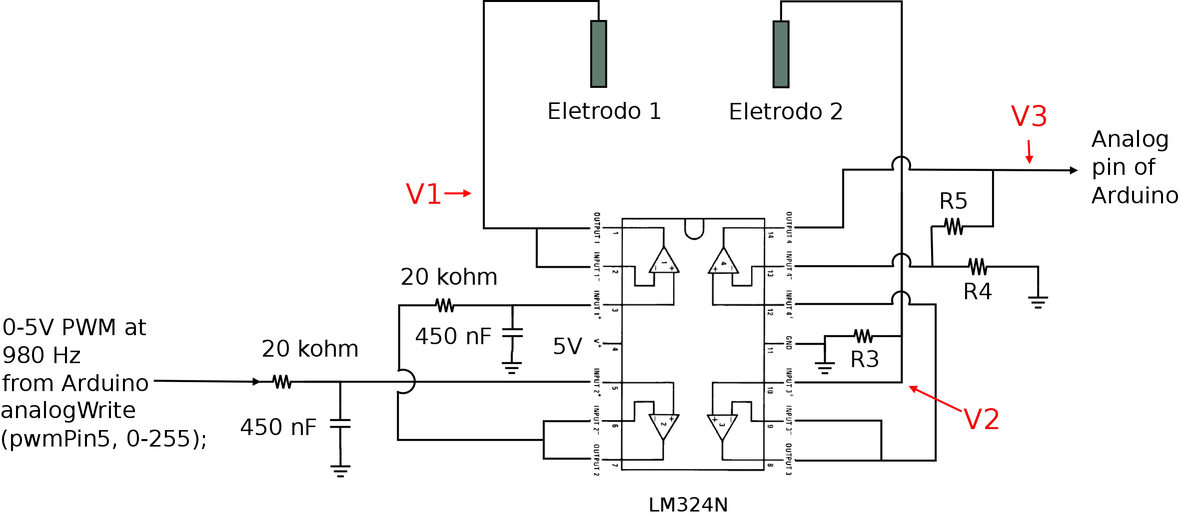
Na figura 124 destacamos o potencial em 3 posições do circuito que serão usadas para os cálculos de corrente.
Figura 124. Diagrama do circuito do potenciostato com destaque para os potenciais em 3 diferentes pontos do circuito: V1, V2 e V3.
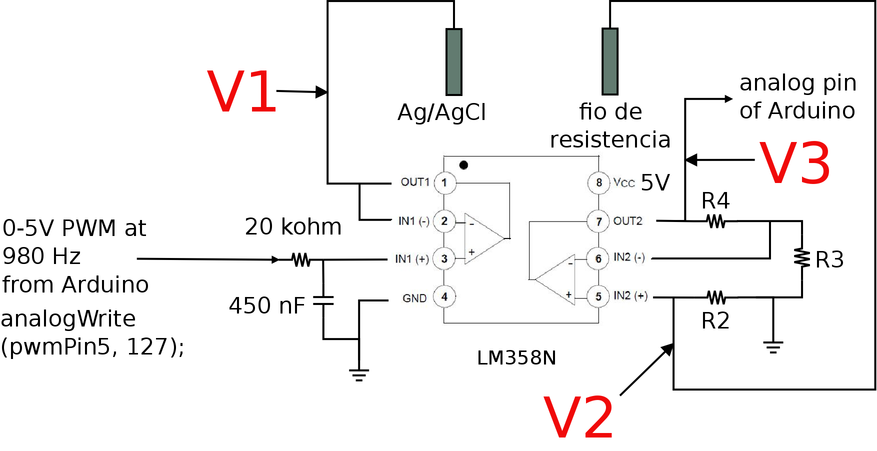
O potencial V1 é o potencial aplicado no eletrodo 1 que, no nosso caso é o eletrodo de Ag/AgCl. O potencial V2 é o potencial do eletrodo 2 que, neste caso, representa o fio da resistência de chuveiro. E o potencial V3 é o potencial amplificado pelo AO na configuração amplificador não-inversor.
O potencial V1 é conhecido e corresponde ao potencial aplicado pelo filtro RC, e o potencial V2 pode ser calculado a partir de V3 pela fórmula 14.
Conhecendo o potencial V2 e o valor da resistência R2 podemos calcular a corrente através de R2 através da Lei de Ohm (Fórmula 15), desconsiderando as perdas pela entrada não inversora do AO no pino 5.
Seguindo as orientações do Prof. Gary Mabbott passamos a planejar novos testes exploratórios para conhecer os recursos do instrumento, da técnica e interpretar os resultados obtidos com as soluções de hipoclorito.
Uma referência que foi útil para comparar com os nossos resultados foi o voltamograma de uma solução de hipoclorito enviada pelo Prof. Gary. (Ver figura 125)
Figura 125. Voltamograma cíclico de uma solução de Hipoclorito de Sódio (0,5%) em meio com 0,1M de NaCl
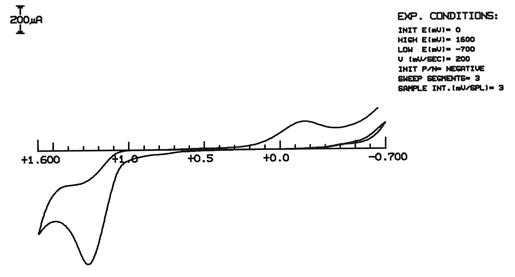
Transcrevo a seguir os comentários originais do Prof. Gary sobre este voltamograma:
Dica
"One can see a strong peak for the oxidation of ClO- to ClO2- beginning around +1.3 V. This cyclic voltammogram was apparently scanned from 0 V in the negative direction first. (If you look closely, you can see that there are 3 lines around -0.6 V)
The first negative-going scan shows no current near -0.18 V, but after the electrode is scanned out to +1.3 V and beyond, it is scanned back in the negative direction to reveal a new peak at -0.18 V for the reduction of ClO2- to Cl- .
Fizemos as seguintes mudanças ness nova série de testes:
Aumentar a concentração do eletrólito de suporte (NaCl) de 3,4×10-3 M para 0,1 M (5,84 g/L).
Aumento da amplificação trocando R4 por um resistor de 1MΩohm.
Tabela 14. Soluções de Cloro Livre para testes com o potenciostato.
| Número da solução | mgCl2/L |
|---|---|
| 0 | 0 |
| 1 | 2,7 |
| 2 | 5,5 |
| 3 | 10,9 |
| 4 | 21,9 |
| 5 | 43,9 |
| 6 | 87,9 |
| 7 | 175 |
| 8 | 351 |
| 9 | 703 |
| 10 | 1406 |
Fizemos varreduras com as soluções de 0 mgCl2/L a 703 mgCl2/L, com velocidade de varredura de 100mV/s e taxa de amostragem de 100 leituras / patamar, em meio contendo 0,1 M (5,84 g/L) de NaCl. Os resultados estão apresentados na figura 126
Figura 126. Voltamogramas das soluções de hipoclorito 0 mgCl2/L a 703 mgCl2/L, em meio contendo 0,1 M (5,84 g/L) de NaCl.
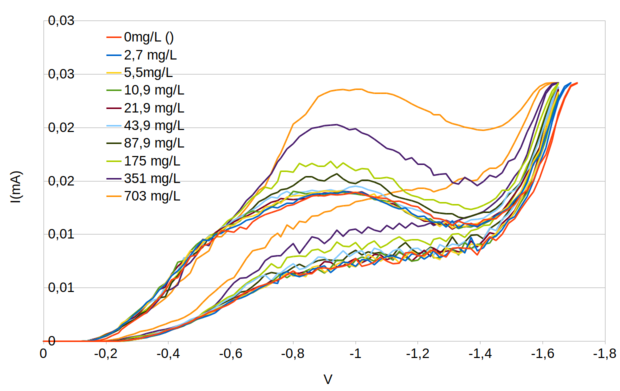
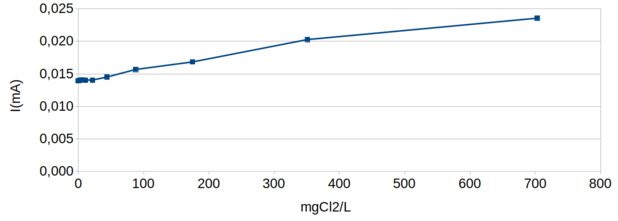
A figura 127 mostra a relação do pico de corrente, na região entre 0 V e -1,4V, com a concentração de Cloro Livre.
Estamos usando uma fonte única ou unipolar portanto são aplicados potenciais positivos, em relação à terra, no eletrodo de Ag/AgCl.
O eletrodo Ag/AgCl é conectado ao pino 1 (OUT1) do LM358 onde é aplicado o potencial positivo gerado pelo filtro RC. E o eletrodo metálico é conectado ao pino 5 (IN2 +) do LM358, e é conectado ao R2, que por sua vez é conectado ao terra, como mostra a figura 124.
Então, podemos entender que o eletrodo de Ag/AgCl é um ânodo onde ocorre a reação de oxidação da prata:
E o eletrodo metálico está funcionando como um cátodo onde ocorre a redução do hipoclorito (ou outras espécies redutíveis):
Portanto, são os elétrons drenados da terra (na direção oposta à corrente convencional) que reduzem as espécies redutíveis na superfície do eletrodo metálico. E são compensados pelos elétrons liberados para o circuito pela oxidação do metal prata no eletrodo positivo de Ag/AgCl.
Dessa forma, para realizar a oxidação do hipoclorito deveríamos inverter a posição dos eletrodos, conectando o eletrodo de metal como um pólo positivo e o eletrodo de Ag/AgCl próximo ao aterramento.
Por convenção, o sinal dos potenciais no voltamograma são considerados sob o ponto de vista do eletrodo de trabalho, que no nosso caso é o eletrodo metálico. Quando aplicamos +1V ao eletrodo de referência, ele puxa cargas negativas da solução segundo a reação 16.
Isso torna o potencial eletroquímico da solução mais positivo, e nessas condições o eletrodo de trabalho (ligado ao terra por R2) parece estar com um potencial mais negativo em comparação com a solução. Nessas condições, para evitar confusão, os eletroquímicos seguem a convenção de rotular o eixo de potencial com valores negativos. Por isso passamos a adotar potenciais negativos no gráfico da figura 126.
Outra convenção é considerar que as correntes catódicas como positivas e as correntes anódicas como negativas.
Outra sugestão do Prof. Gary foi avaliar o comportamento do pico de corrente em função da velocidade de varredura (scan rate) conforme a seguinte transcrição:
Dica
There are a few other things that you should be able to demonstrate that would indicate that the peak current is due to the analyte in solution. One of those is that a plot of the peak current as a function of the square root of the scan rate (at a fixed concentration of hypochlorite) should be linear. That is true when the only current source is the oxidation of the analyte as it diffuses to the electrode surface (no stirring).
Se houver adsorção das espécies eletroativas na superfície do eletrodo, o pico de corrente será diretamente proporcional à velocidade de varredura. E se as reações forem o resultado de processos reversíveis de transferência de elétrons com espécies que se difundem livremente na solução o pico de corrente será proporcional à raiz quadrada da velocidade de varredura, segundo a equação de Randles-Sevcik.
Dica
Alguns links que discutem a dependência do pico de corrente com a velocidade de varredura: Important parameters in CV, Why peak current Vs square root of scan rate is not linear?, A Practical Beginner's Guide to Cyclic Voltammetry.
Fizemos uma sequência de varreduras com uma mesma solução, variando a velocidade de varredura (scan rate) (Figura 128) para testar se as espécies eletroativas estão adsorvidas na superfície do eletrodo ou se sofrem difusão livre na solução.
Figura 128. Varreduras com diferentes velocidades feitas com a solução de 175 mg/L de Cloro Livre, com taxa de amostragem de 100, meio com NaCl 0,1M, R2=197Ω, R3=957 Ω e R4=1003000 Ω
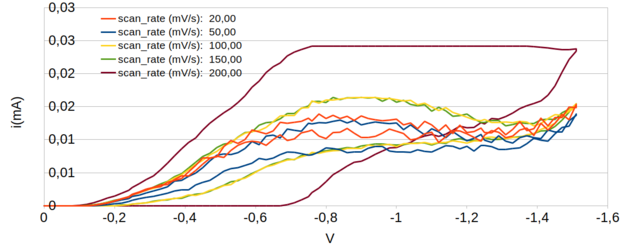
Os voltamogramas não indicam muita variação na posição da corrente de pico com a velocidade de varredura, mas antes de dar continuidade a novos testes usando o eletrodo de Ag/AgCl como ânodo, resolvi avaliar a possível substituição do eletrodo de Ag/AgCl por um eletrodo de grafite.
Um dos motivos é a “sensibilidade” do eletrodo de Ag/AgCl para altas correntes, como alertou o Prof. Gary:
"Your question about reversing the polarity after analysis to reduce silver ions back to silver metal at the reference electrode is a good one. My answer is basically, no. But there are lots of things to consider here. Many of these issues depend on size. By making some wise choices about size of electrodes and size of currents, you can avoid a lot of problems. In the extreme, running lots of current through the reference electrode can consume all of the metallic silver and you are left with no electrode. Even before you get to that point you can have significant changes in the surface structure and chemistry that damage it. The change in surface chemistry may shift its potential away from its reference value. If that happens, your working (or indicator) electrode is no longer at the potential that you wanted for the electrolysis of the analyte."
Ou seja precisamos ter cuidado com as correntes para não danificar o eletrodo de Ag/AgCl.
Os testes que foram feitos até este momento se concentraram na redução do íon OCl- segundo a reação 17, e como par redox a oxidação da prata segundo a reação 16.
No entanto o voltamograma da figura 125 mostra que é possível uma reação de oxidação do íon hipoclorito.
Além disso encontramos o artigo Electrochemical Detection of Free Chlorine Using Anodic Current que mostra o uso de reações de oxidação do íon hipoclorito para análise quantitativa.
Então pensamos em usar um eletrodo de grafite ligado no polo positivo para funcionar como ânodo e oxidar o íon ClO- a ClO2- (ou ClO3-), e o eletrodo metálico ligado ao polo negativo para funcionar como cátodo reduzindo o íon ClO- a Cl-.
Dessa forma teríamos um par redox que permitiria a geração de correntes proporcionais à concentração de ClO- sem o uso de um eletrodo “sensível” a altas correntes como o Ag/AgCl.
Para testar essa hipótese montei um eletrodo de grafite dentro de uma seringa de insulina, mantendo para fora uma pequena área em contato com a solução como mostra a figura 129)
Fizemos então alguns testes exploratórios com o par grafite (ânodo) e metal (cátodo) e o voltamograma no intervalo de 0-1V está na figura 130)
Figura 130. Voltamograma de 0-1V usando um eletrodo de grafite como ânodo e um eletrodo metálico como cátodo.
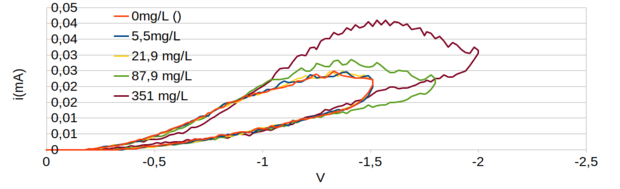
Com esse novo par de eletrodos fizemos algumas medidas para testar a redução da corrente do branco (background) usando uma técnica muito interessante que foi sugerida pelo Prof. Gary e está transcrita a seguir:
... Part of the problem is the background current at high scan rates. ... There are ways of eliminating much of the background current. Most of the background current is associated with the charging of the electrical double layer at the working electrode surface. Basically, the double layer of ions on the solution side vs. electrons at the electrode at the solution interface acts as a capacitor. When your device changes the applied potential, some current is required to charge up the capacitor at this interface. Your current measurement gets the total current. The charging current can easily be bigger than small electrolysis currents. You can avoid much of this unwanted charging current by changing the way you apply the voltage to the non-inverting input of OA1.
Instead of applying a voltage that changes linearly with time, you can program the voltage at that point to step in small increments (something between 5 and 25 mV per step). The current will surge at the working electrode as the voltage steps, but (depending on the cell resistance and the capacitance of the double layer) this charging current will decrease rapidly to zero in a few milliseconds. In 0.1 M NaCl using a 3 mm circular disk electrode, the current dies out in about 5 ms. The strategy would be to step the voltage, then wait about 10 ms before measuring the current. Then, store the sampled current. Then repeat the process to the next voltage until you scan over the entire voltage window. The voltammogram is plotted from the sampled current values vs. the applied voltage. This strategy helps lower the background current to a level where you should be able to see the diffusion controlled current from the hypochlorite.
Para implementar essa técnica de leitura vamos primeiro fazer alterações no código do Arduino para identificar o padrão de variação da corrente com as variações no potencial ao longo do voltamograma.
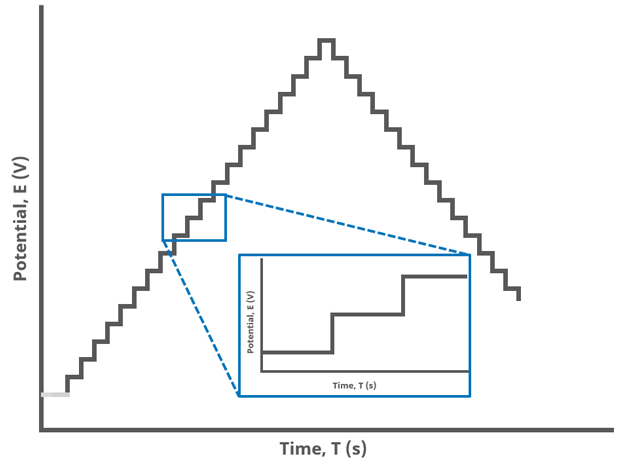
A variação de potencial, gerada pelo filtro RC, no circuito da figura 124 apresenta um perfil de variação conhecido por Voltametria em Escada como mostra a figura 131.
Mas para avaliar o padrão de variação do potencial no cátodo em cada patamar de potencial do voltamograma fizemos leituras do potencial em intervalos de microsegundos utilizando uma variável do tipo array. A seguir alguns trechos do código:
...
//Set the number of samples at each level of potential
const byte num_samples = 100;
//To calculate the average_vo the num_samples in type float
float divisor = 100.0;
float instant_vo[num_samples + 1];
unsigned long time_instant_vo[num_samples + 1];
...
//Start to count time of scan
unsigned long StartTime = micros();
for (pwm = pwm_min; pwm <= pwm_max; pwm++){
analogWrite(pwm_output_5, pwm);
for (int i=0; i < num_samples; i++) {
instant_vo[i] = analogRead(analog_input_0) * 5.0 / 1023.0;
unsigned long CurrentTime = micros();
time_instant_vo[i] = CurrentTime - StartTime;
delay(interval/num_samples);
}
vi = pwm * 5.0 / 255.0;
for (int i=0; i < num_samples; i++) {
Serial.print(i);
Serial.print(";");
Serial.print(vi);
Serial.print(";");
//Serial.println(average_vo);
Serial.print(time_instant_vo[i]);
Serial.print(";");
Serial.println(instant_vo[i]);
}
}
O gráfico da figura 132 mostra a variação do potencial de saída (Vo) ao longo do tempo (ms), para os potenciais aplicados (Vi) de 0,35mV, 0,45mV e 0,55mV, referentes ao voltamograma 130.
Figura 132. Variação do potencial de saída (Vo) em milisegundos para os potenciais aplicados (Vi) de 0,35mV, 0,45mV e 0,55mV, referentes ao voltamograma 130.
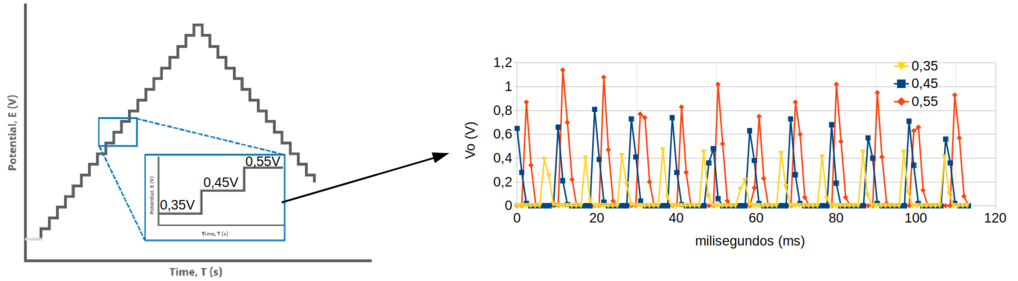
O gráfico mostra o padrão de variação do potencial em um intervalo de ~110 ms indicando a grande oscilação das leituras. Essa variação é coerente com a oscilação no potencial aplicado (pelo filtro RC) como pode ser visto nas leituras do osciloscópio na figura 112.
Devido a essa oscilação tivemos que aumentar a taxa de amostragem para 200 amostras por patamar e isso acaba comprometendo a sensibilidade do potenciostato para detectar sinais em baixas concentrações de cloro livre. Pois quanto maior o desvio padrão (s) das leituras maior o Limite de Detecção (LD) do método que pode ser definido como LD = 3×s
Em seguida fizemos vários voltamogramas avaliando o efeito de diferentes “tempos de espera”, para o início das leituras, na intensidade do pico de corrente. E o gráfico da figura 133 mostra uma redução significativa do sinal até o limite de 20 ms. A partir daí as reduções foram pequenas e constantes.
Figura 133. Voltamogramas (Vi) X (Vo) de uma mesma amostra com diferentes tempos de espera (0 ms, 5 ms, 10 ms, 15 ms, 20 ms, 25 ms e 30 ms).
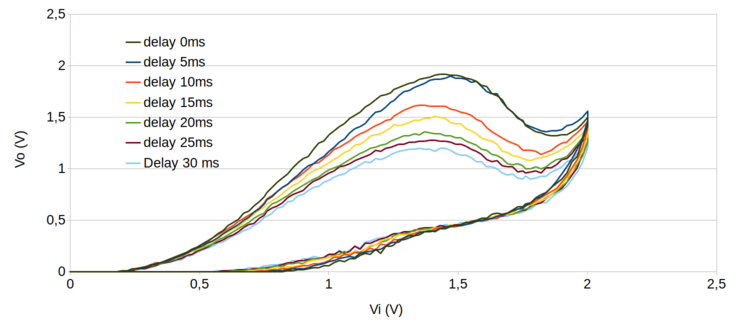
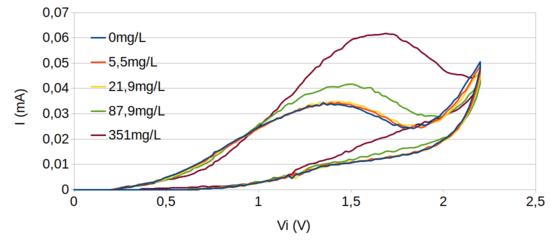
Com esses resultados fizemos alguns voltamogramas com o par de eletrodos grafite(cátodo)/metal(ânodo) em diferentes concentrações de cloro livre e obtivemos os voltamogramas da figura 134.
Figura 134. Voltamogramas (I) X (Vi) do par de eletrodos grafite(cátodo)/metal(ânodo), R2 = 197 Ω R3 = 957 Ω R4 = 198000 Ω (circuito 113), meio com 0,1M de NaCl, taxa de amostragem de 200 leituras por patamar de potencial e diferentes concentrações de cloro livre.
Por que o eletrodo de trabalho deve ter pequena área de contato com a solução?
A voltametria está baseada na medida de uma corrente que se desenvolve em uma célula eletroquímica sob condições de polarização completa por concentração. Nessas condições a corrente limite (voltametria hidrodinâmica) e o pico de corrente (voltametria cíclica com a solução em repouso) são diretamente proporcionais à concentração do reagente.
Por isso o ideal é manter a área do eletrodo de trabalho a menor possível para favorecer a sua polarização.
E qual a utilidade do eletrólito de suporte (Ex: NaCl 0,1M)?
Em voltametria procura-se minimizar o fenômeno de migracao adicionando um excesso de eletrólito inativo. Quando a concentração do eletrólito de suporte supera a do analito em 50 a 100 vezes, a fração da corrente total conduzida pelo analito se aproxima de zero. Em virtude disso, a velocidade de migração do analito em direção ao eletrodo de carga oposta torna-se essencialmente independente do potencial aplicado.
Mas por que evitar a migracao?
No artigo Recent Advances in Voltammetry encontramos a seguinte explicação:
The vast majority of electrochemical experiments are carried out in the presence of a large excess of inert, fully dissociated electrolyte.78 The purpose of this electrolyte is to generate a high ionic strength in solution, which will efficiently dissipate the excess charge necessarily introduced into solution via electrolysis, and suppress the resultant electric field. There are two main reasons that this is normally the case.
The first reason is to prevent ohmic drop. The driving force behind electron transfer is the potential difference between the electrode and the point in solution where electron transfer takes place, ϕm + ϕs. The bulk solution, far from the electrode, has some fixed potential ϕbulk. If the potential drop between ϕm and ϕbulk occurs over a distance greater than the electron tunneling distance for electron transfer (outside the zone of electron transfer, ZET - Zone of Electron Transfer) then the full driving force will not be felt; the potential difference is lowered as a result of ohmic drop.
If a large amount of excess electrolyte is added to efficiently dissipate excess charge, the distance over which the drop between ϕm and ϕbulk is compressed to a distance much smaller than the ZET. This being the case, the electron transfer is then driven by the maximum potential difference, ϕm and ϕbulk. This is exemplified schematically in Figure 135.
Figura 135. Schematic representation of solution potential profiles under conditions of high (solid line) and low (dashed line) support. The dotted lines represent the zone of electron transfer extending from the electrode surface out a certain distance into solution.
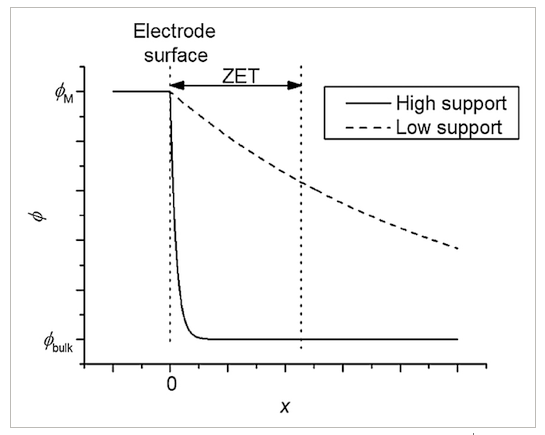
The solid line shows the potential profile under conditions of high support (a large excess of supporting electrolyte), which is compressed to short distances and does not extend very far into the ZET. The dashed line shows low support conditions (small amounts of supporting electrolyte), where the electric field extends out beyond the ZET, resulting in a smaller driving force for electron transfer.
Secondly, a compressed electric field will eliminate migratory effects from the mass transport of solution phase species.128 If an electric field extends far beyond the electrode surface, the resulting potential gradient in solution will induce electrical migration of charged species, in addition to diffusion.
Nota
The majority of analytical theory in electrochemistry assumes diffusion-only conditions, and the presence of migration complicates matters. For these two reasons, excess supporting electrolyte is usually added to an electrochemical experiment. However, migration effects can offer extra kinetic and mechanistic information unavailable at high support levels.129 For this reason, it may be desirable to carry out electrochemical experiments where a small amount, or zero, supporting electrolyte is added to solution. For such experimental cases new theoretical models are needed to describe the experiments and allow the experimental electrochemist to interpret results.
E mais adiante é feito o seguinte comentário:
In general the lack of supporting electrolyte leads to the cyclic voltammetry becoming sensitive to the charge of the reactants, intermediates, and product species.
Ou seja, o uso de um eletrólito de suporte elimina o efeito de migração por uma "conveniência interpretativa". Mas a presença dos efeitos de migração podem fornecer "informações adicionais" que podem ser úteis se forem "devidamente processadas"...
Por que a área do “contra eletrodo” (ou eletrodo auxiliar) é maior do que a área do eletrodo de trabalho?
Transcrevo a seguir a resposta para essa pergunta do site Tips of Voltammetry.
3.7. Area of counter electrode
An electrochemical response is observed as a sum of the half reactions at the two electrodes. In order to extract the reaction at the working electrode, a conventional technique is to increase the area of the counter electrode so that the reaction at the counter electrode can be ignored. If the counter electrode area is increased by 20 times the area of the working electrode, the observed current represents the reaction of the working electrode with an error of 5%.
Conventional CV is typically performed in solutions with analyte concentrations in the 0.1-200 mM range. Eq. (5.31) indicates that the peak current increases as the square root of scan rate. Why not scan faster in order to obtain better sensitivity? The problem is that the background current increases linearly with scan rate. The background can eventually overwhelm the desired signal at high scan rates. At lower concentrations, the signal looks small compared to the background current. Section 5.4 discusses special techniques that are better suited for quantitative analysis in dilute solutions. (Electroanalytical Chemistry, Principles, Best Practices and Case Studies, 1st Edition, 2020)
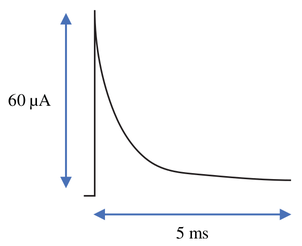
A large fraction of the background current is associated with charging the double layer. The double layer charging occurs quickly and generally decays to zero after the first few milliseconds. The current response to a 10 mV potential step at a carbon disk electrode in a clean electrolyte solution is shown in figure 136.
Figura 136. Corrente de carregamento da dupla camada em um eletrodo de disco de carbono com 3 mm de diâmetro em uma solução contendo 0,1 M KCl solution com pulso de 10 mV e sem espécies eletroativas presente. (Electroanalytical Chemistry, Principles, Best Practices and Case Studies, 1st Edition, 2020)
Como se pode ver pela figura 134 o pico de corrente só começa a se diferenciar do sinal do branco no intervalo de concentração entre 22 e 88 ppmCl2.
O gráfico da figura 132 mostra as grandes variações do potencial de saída (Vo) ao longo do tempo (ms), em cada patamar de potencial, o que é consistente com as oscilações do potencial aplicado como se pode ver no perfil do sinal de saída do filtro RC (Figura 112) quando aplicamos um sinal PWM produzido pelo Arduino com largura de pulso de 50%, produzido pelo comando analogWrite(pwmPin5, 127);.
Essas oscilações no potencial aplicado afetam as leituras como já havia alertado o Prof. Gary:
...the PWM technique is based on an average voltage at a digital pin. It is interrupted before it can charge up to the full +5V. It drifts some before it is pulsed again. One does see a voltage at this pin that near the target value, but it is actually oscillating up and down by a small amount. If you try to measure small current signals with this oscillating applied voltage, it will induce an oscillation in the double layer charging (background) current in the electrochemical cell. That will be noticeable and it will interfere with the signal current from the hypochlorite. A DAC output will provide a steady voltage and will give you a lot of flexibility in your experiments.
Mas antes de investir na compra e implantação de um módulo DAC resolvemos fazer algumas modificações no circuito para tentar reduzir essas oscilações e incluímos mais um AO como mostra a figura 137.
Figura 137. Circuto para a conversão do sinal PWM em um sinal analógico estável onde R1 e R2 = 20kΩ, C1 e C2 = 450 nF e frequência do pulso PWM = 980Hz.
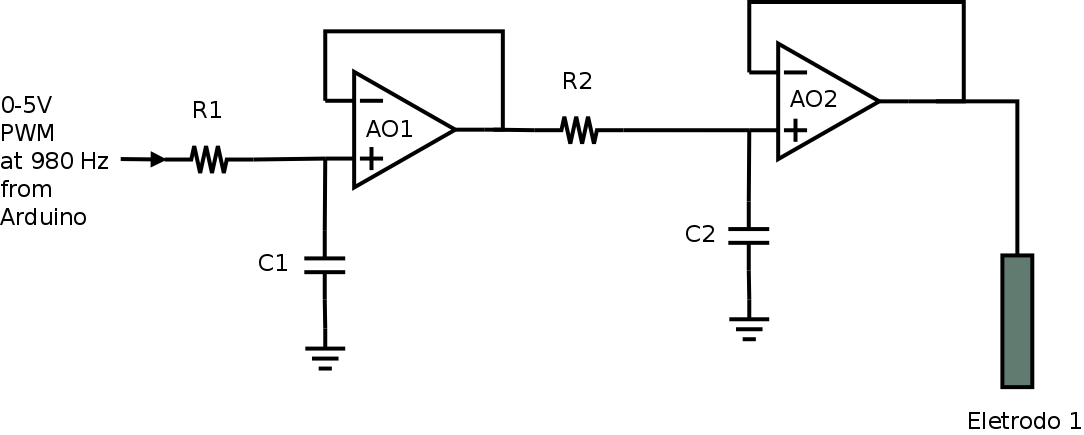
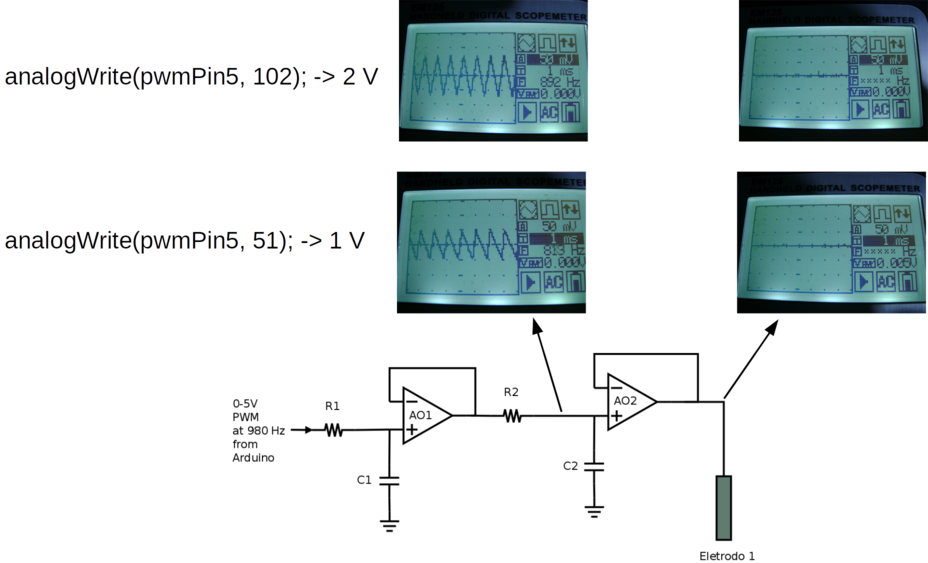
As medidas com osciloscópio mostram que o segundo filtro RC foi capaz de remover as oscilações gerando um potencial com estabilidade satisfatória para medidas voltamétricas como mostra a figura 138.
Figura 138. Testes para avaliar a capacidade do circuito da figura 137 em converter o sinal PWM do pino digital do Arduino em um potencial estável.
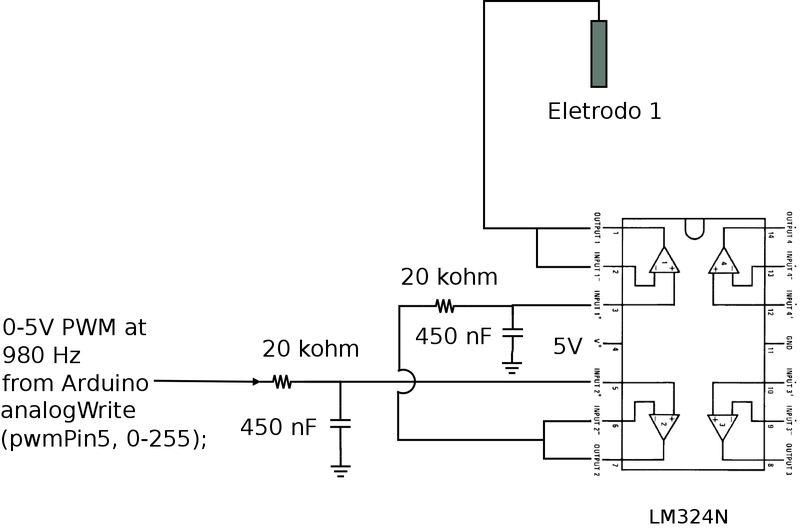
Substituímos o CI LM358N (com dois AOs) pelo CI LM324N (com 4 AOs) e usamos 2 AOs para fazer a conversão do sinal PWM em um sinal analógico estável como mostra a figura 139.
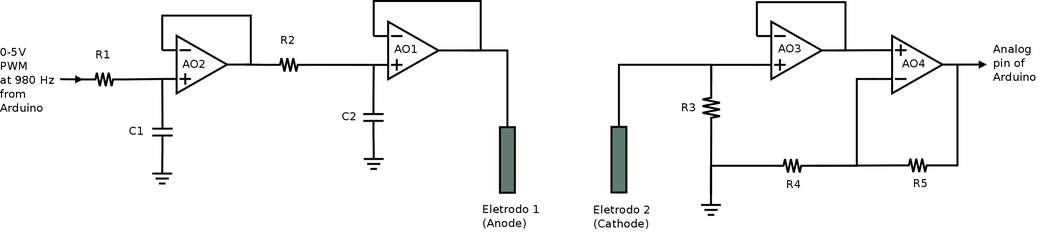
Os dois AOs restantes do CI LM324N foram usados para fazer as leituras de corrente conforme o diagrama da figura 140. O AO3 foi usado como um seguidor de voltagem e o AO4 como um amplificador não-inversor.
O potencial V1, aplicado no eletrodo 1, é definido pelo pulso PWM gerado pelo pino digital do Arduino. O potencial V2 é o potencial do eletrodo 2, em relação ao terra. E o potencial V3 é determinado pelo conversor ADC do Arduino. A corrente “I” que circula pelos eletrodos pode ser calculada pela equação 18).
A diferença de potencial “efetiva” entre os eletrodos 1 e 2 corresponde à diferença V1 − V2.
Para facilitar a realização de medidas com o potenciômetro começamos a desenvolver uma interface gráfica de controle usando a linguagem Tcl/Tk que permita definir os parâmetros de varredura, a exibição do voltamograma e o armazenamento dos dados.
Requisitos iniciais do programa:
definir os parâmetros de varredura: potencial inicial e final (scan_range), velocidade de varredura (scan_rate), taxa de amostragem (sampling_rate) e tempo de espera para aquisição (delay_time)
executar a varredura (startScan)
exibir o gráfico do voltamograma (plotGraph)
gravar as leituras de IxV (saveData), e/ou a imagem do gráfico (exportGraph)
remover as leituras de IxV (clearData), e/ou a imagem do gráfico (clearGraph)
Implementamos inicialmente a classe Potentiostat para representar o instrumento, a classe Voltammogram para representar o voltamograma, a classe dataReader para gerenciar a comunicação serial com a placa Arduino, a classe dataKeeper para armazenamento temporários dos dados e a classe controllerPotentiostat para funcionar como uma interface entre o usuário e a classe Potentiostat, como mostra a figura 142).
Como estamos usando AOs que operam com fonte simples só será possível aplicar potenciais positivos nos eletrodos. E dessa forma o eletrodo que for usado como “eletrodo de trabalho” (com menor área) só “poderia” ser usado exclusivamente como cátodo ou ânodo durante uma varredura.
Para contornar essa limitação, pretendemos experimentar uma solução “não convencional” usando um relê com 2 Pólos, 2 Posições e 8 Terminais para fazer a “troca” de polaridade dos eletrodos.
Prevendo esse recurso, vamos incluir as variáveis change_electrode_polarity (0 ou 1), para indicar se haverá mudança da polaridade do eletrodo, e a variável working_electrode (-1 -> cátodo, +1 -> ânodo) para indicar qual a função eletroquímica do eletrodo de trabalho durante o voltamograma.
Para estruturar o fluxo de dados entre o programa e a placa Arduino, planejamos a implementação de classes especializadas nas operações de leitura (dataReader), armazenamento temporário (dataKeeper) e exibição (dataPlotter).
Podemos ter a sequência de criação e “conexão” dos objetos após a criação da interface gráfica do programa como mostra a figura 143).
Criação da instância de dataTable
Criação da instância de dataReader
Criação da instância de dataKeeper
Criação da instância de Potentiostat
Conecta dataReader com Potentiostat
Conecta dataKeeper com Potentiostat
Conecta dataTable com Potentiostat
Cria a instância de controllerPotentiostat
Conecta controllerPotentiostat com Potentiostat
As leituras (I×V) recebidas pela porta serial são exibidas na tabela, mas a atualização do gráfico pode estar ativada ou desativada para permitir fazer testes e receber dados diferentes da estrutura I×V. Por isso criamos a variável plot_data para indicar se os dados recebidos devem ou não ser exibidos no gráfico.
Os gráficos poderão ser individuais ou sobrepostos, permitindo visualizar de forma rápida o efeito de diferentes parâmetros na sensibilidade.
Criamos o atributo status na classe Potentiostat para indicar o modo de operação do instrumento e habilitar ou desabilitar eventos.
Possíveis estados do instrumento:
UNCONNECTED - status inicial default
DEVICE_CONNECTED - placa Arduino conectada
NO_DEVICE - placa Arduino ainda não foi conectada e portanto não existe o device /dev/ttyACM#
SERIAL_ERROR_OPEN - placa já foi conectada mas houve erro na abertura da porta
IDLE - instrumento está conectado e pronto para ser usado
READING - instrumento em uso
Para permitir diferenciar os dados dos comentários, nas mensagens enviadas pelo Arduino, decidimos incluir o caracter “#” em todas as linhas de comentários enviadas pela placa Arduino.
Para organizar o código definimos 3 níveis de atuação para os objetos das classes controllerPotentiostat, Potentiostat e dataReader:
Atribuímos ao objeto da classe controllerPotentiostat o nível 1 (mais próximo ao usuário) e portanto as rotinas de coleta e validação dos parâmetros de configuração que serão enviados para o objeto da classe Potentiostat que está no nível 2. Este irá repassar os parâmetros necessários para os objetos das demais classes em níveis inferiores (3 ...), como por exemplo o objeto da classe dataReader.
Por “nível mais alto” nos referimos aos módulos que interagem mais diretamente com os eventos gerados pelo usuário.
Por exemplo, para realizar uma varredura é necessário estabelecer a “conexão” do programa com a placa Arduino clicando no botão “Connect”. Essa ação do usuário desencadeia a seguinte sequência de eventos:
User:
Click button "Connect"
Controller:
connectInstrument
Potentiostat:
getStatus
...
getStatus
Controller:
if status = IDLE
Potentiostat already connected!
...
getStatus
Controller:
if status = NO_DEVICE
...
getStatus
Controller:
if status = ERROR_SERIAL_PORT
...
getStatus
Controller:
else
Potentiostat:
connectSerialPort
Por exemplo, quando o usuário clicar no botão “Start Scan” teremos uma sequência de eventos como mostra a figura 145).
User:
Click button "Start Scan"
Controller:
startScan
Check State
State IDLE?
NO
...
Controller:
startScan
Check State
State IDLE?
YES
Potentiostat:
startScan(Potentiostat)
setState READING
dataReader:
startScan(dataReader)
Open serial port (getID_port)
Link data at id_port to keepReadout of dataKeeper
Schedule the startReading after time
Schedule the checkComunication after timeout
Ao solicitar uma conexão o controlador chama o método connectSerialPort do Potentiostat, que repassa a chamada para o dataReader. A abertura da porta serial é feita pelo dataReader, mas o controlador localiza o device ACM. No futuro podemos implementar na interface a possibilidade do usuário definir o número para o ACM. Após conectado precisamos estabelecer a sequência de eventos para o startScan. O controlador coleta os parâmetros de configuração e chama o método startScan no potentiostat, passando os parâmetros de configuração atualizados. O potenciostato chama dataReader que deve criar o vínculo de dataKeeper com a porta serial através do comando fileevent. Dessa forma tudo que chegar pela porta serial será armazenado por dataKeeper. O potenciostato envia os parâmetros para o dataReader que escreve na porta serial. envio do comando startScan e ativação do loop de atualização das leituras a cada 1 ou 2 segundos Podemos criar uma fila de comandos no dataReader para controlar os intervalos entre os diferentes comandos: scan_range, sampling_rate, delay_sampling etc. Um dos primeiros eventos de startScan deve ser a criação do vínculo de dataKeeper com a porta serial através do comando fileevent. Dessa forma tudo que chegar pela porta serial será armazenado por dataKeeper. A inserção dos dados na tabela (dataTable) poderá ser feita por dataReader ou por potentiostat. Mas qual deles escolher? Vamos deixar a manipulação (processamento inicial) dos dados para o dataReader e deixar para o potentiostat as tarefas de mais alto nível como inserir na tabela e na gráfico. Dessa forma dividimos as tarefas entre os diferentes agentes. O potentiostat pode ativar em dataReader a tarefa de resgatar os dados acumulados em dataKeeper e transferir diretamente para dataTable. E o próprio dataReader verifica a mensagem de final de varredura, desativa o loop e notifica potentiostat. DataReader também deve verificar eventuais mensagens de erro. Mas como notificar a interface sobre a mudança de status durante a leitura (IDLE -> READING e READING -> IDLE). Podemos passar para as instâncias em níveis inferiores, o objeto demandante e retornar uma chamada para o demandante informando a mudança de status. Poderíamos usar um semáforo, mas nesse caso os objetos teriam que ficar monitorando a mudança de status de uma variável. Percebi a ocorrência de algumas falhas na comunicação entre o programa e o Arduino e implementei o método de checagem checkCommunication na classe dataReader que apenas verifica se foi recebida alguma resposta pela porta serial dentro do intervalo de tempo da variável timeout. Próximas etapas: -radiobutton para ativar ou desativar a exibição das leituras de I x V no gráfico (voltamograma) -remover e salvar o gráfico -envio dos parâmetros de configuração da porta serial para o objeto de dataReader para configurar o potenciostato e pedir confirmação antes de iniciar uma varredura -modificar o sketch no Arduino para incluir # nos comentários e definir a função set_scan_rate -implementar módulo com equação para converter as leituras de potencial (V) em corrente (I) antes de exibir no gráfico I x V 28/04/2021 Implementada a função setDelaySampling no sketch do Arduino no arquivo potenciostato_07 29/04/2021 Ajustar o intervalo entre cada amostragem em microsegundos usando o comando delayMicroseconds(N); time_left (for sampling) = interval - delay_time interval_between_sample = time_left / number_samples Electroanalytical Chemistry, Principles, Best Practices and Case Studies, 1st Edition, 2020 The distance from the surface to the outer edge of the diffuse region is known as the Debye length, lambda D . The Debye length is inversely proportional to the square root of the electrolyte concentration. A good benchmark to keep in mind is that the Debye length is about 100 Å (10 nm) for a sodium chloride solution of 0.01 M [9]. Most electroanalytical measurements are made at electrolyte concentrations of 0.01 M or higher. This profile for the potential has an important significance for voltammetry experiments where molecules must be transported to the electrode surface in order to exchange electrons with the surface. In most cases, the molecules can approach no closer than the OHP. Consequently, the electric potential that they experience is that of the OHP rather than the true potential of the electrode surface. As will be discussed in Chapter 5, this has important implications for the rate of electron transfer and the magnitude of the corresponding current in voltammetry experiments. One of the most widely used methods for avoiding background current is called square-wave voltammetry (SWV). The SWV-applied voltage pattern appears in Figure 5.17c. It is helpful to think of the pattern as a pulse sitting on the rising edge of each step of a voltage staircase. The current is sampled twice during each step, once near the end of the voltage pulse and again after the voltage comes down off of the pulse (shortly before stepping up again). 1.4.2. The Relationship Between Double Layer Charge and the Potential at the Electrode Interface ELECTROANALYTICAL CHEMISTRY Principles, Best Practices, and Case Studies Gary A. Mabbott Próximas etapas: Providenciar melhorias no potenciostato incluindo um seguidor de voltagem associado a um outro filtro RC para reduzir a oscilação. Podemos também incluir um divisor de tensão para melhorar a resolução. Os testes serão feitos em dois pH distintos: tampão 0,1M acético/acetato (pH ~4.6) e tampão 0,1M carbonato/bicarbonato (pH ~10) No meio ácido vamos avaliar a redução da forma ácida (HClO), e no meio básico vamos avaliar a redução da forma ácida (HClO) Os testes serão feitos com os seguintes arranjos de eletrodos: 1 - cátodo e ânodo de grafite 2 - cátodo e ânodo de nichrome 3 - cátodo de grafite e ânodo de nichrome 4 - ânodo de grafite e cátodo de nichrome 5 - cátodo e ânodo de aço inox Tampão de carbonato/bicarbonado https://www.aatbio.com/resources/buffer-preparations-and-recipes/carbonate-bicarbonate-buffer-ph-9-2-to-10-6 para o prepara de tampão carbonato bicarbonato para as reações de oxidação de hipoclorito em pH 10 seguindo as dicas do artigo Linear sweep voltametric determination of free chlorine in waters using graphite working electrodes. Tampão de acético/acetato https://courses.lumenlearning.com/wsu-sandbox2/chapter/buffers-2/ http://microscopy.berkeley.edu/Resources/instruction/buffers.html https://www.sigmaaldrich.com/life-science/core-bioreagents/biological-buffers/learning-center/buffer-reference-center.html#sodiumacetate https://www.aatbio.com/resources/buffer-preparations-and-recipes/acetate-buffer-ph-3-6-to-5-6 Vídeo didático sobre um sensor amperométrico que usa um cátodo de ouro e ânodo de Ag/AgCl https://www.youtube.com/watch?v=dxkp-VnJ1FU 29/03/2021 Diante da necessidade de se gerar uma sinal analógico estável passamos a analizar os conversore DAC (Digital Analogic Converter) que poderiam ser usados para essa finalidade. Os principais componentes utilizam o protocolo de comunicação I2C para se comunicar com o Arduino, por isso passamos a pesquisar como implementar esse protocolo de comunicação: https://www.arduino.cc/en/Reference/Wire https://www.instructables.com/Arduino-and-I2C/ https://learn.adafruit.com/mcp4725-12-bit-dac-tutorial Lojas: https://www.arducore.com.br/modulo-mcp4725-i2c-conversor-digital-analogico https://www.arduoeletro.com/mcp4725-conversor-digital-analogico-dac-arduino-pic-etc https://www.usinainfo.com.br/conversor-ad-da-arduino/conversor-digital-analogico-dac-mcp4725-3418.html https://www.baudaeletronica.com.br/conversor-dac-digital-analogico-mcp4725-i2c.html https://www.filipeflop.com/produto/conversor-digital-analogico-dac-mcp4725-i2c/ Potentiostat Notes 2: Software https://publiclab.org/notes/JSummers/12-20-2013/potentiostat-software Pencil graphite as electrode platform for free chlorine sensors and energy storage devices https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0248142 Electrochemical Water-Splitting Based on Hypochlorite Oxidation https://pubs.acs.org/doi/10.1021/jacs.5b02087 Review-Pencil Graphite Electrode: An Emerging Sensing Material https://iopscience.iop.org/article/10.1149/2.0012003JES/pdf Modified pencil graphite electrode as a low-cost glucose sensor https://doi.org/10.1016/j.jsamd.2020.07.004 Development of an Electrochemical Sensor Using Pencil Graphite Electrode for Monitoring UV-Induced DNA Damage https://doi.org/10.1021/acs.jchemed.9b01065 Pencil Graphite Electrodes: A Versatile Tool in Electroanalysis https://doi.org/10.1155/2017/1905968 Polymer lead pencil graphite as electrode material: Voltammetric, XPS and Raman study https://doi.org/10.1016/j.jelechem.2016.11.030 Which pencil lead is best for making electrode? https://www.researchgate.net/post/Which-pencil-lead-is-best-for-making-electrode Site com AOs mais sensív eis: http://www.tiggercomp.com.br/novaloja/product_info.php?products_id=8574 http://www.tiggercomp.com.br/novaloja/product_info.php?products_id=6800 http://www.tiggercomp.com.br/novaloja/product_info.php?products_id=9545 Idéias: Método de análise multivariada que considere diversos parâmetros tais como pico de corrente, posição do pico de corrente, scan_rate Métodos cinéticos que usem um reagente oxidável mais facilmente monitorado pelo cloro https://chem.libretexts.org/Courses/Northeastern_University/13%3A_Kinetic_Methods Préconcentração (membraneless gas-separation ?) Electrochemical detection of free chlorine at highly boron-doped diamond electrodes Cita 8] L. Hammer, G. Wranglén, Electrochem. Acta 9 (1964) 1-16. [9] J. Jin, Y. Suzuki, N. Ishikawa, T. Takeuchi, Anal. Sci. 20 (2004) 205- 207. [10] A.N. Tsaousis, C.O. Huber, Anal. Chim. Acta 178 (1985) 319-323. [11] S. Uchiyama, S. Suzuki, O. Hamamoto, Electroanalysis 1 (1989) 323 - 326. [12] A. van den Berg, K. Koudelka-Hep, B.H. van der Schoot, N.F. de Rooij, E. Verney-Norberg, A. Grisel, Anal. Chim. Acta 269 (1992) 75-79. [13] A. Okumura, A. Hirabayashi, Y. Sasaki, R. Miyake, Anal. Sci. 17 (2001) 1113-1116. Alternativas de amplificadores: https://www.multcomercial.com.br/circuito-integrado-lm310n-dip8-cod-loja-2179-national.html Circuito Integrado CA3130 https://www.soldafria.com.br/circuito-integrado-ca3130-p-1235.html?search=ca31 CA3140 https://www.soldafria.com.br/circuito-integrado-ca3140ez?search=ca31 https://www.newtoncbraga.com.br/index.php/artigos/49-curiosidades/4507-art618.html
Nosso objetivo é dispor de um sistema “automático” para análises eletroquímicas, e um dos componentes necessários é o compartimento onde são feitas as medidas.
Uma etapa necessária é a “homogeneização” dos reagentes antes das medidas, que pode ser feita em “batelada” ou em fluxo.
Em um sistema em batelada é necessário algum tipo de “agitador” (mecânico ou magnético), e em um sistema em fluxo precisamos de uma cela de fluxo. Então resolvi começar a trabalhar na montagem de uma cela de fluxo microfluídica.
Tentei montar um primeiro protótipo como um “sanduíche” de 2 chapas de acrílico com um “recheio” de silicone seguindo as etapas indicadas na figura 146.
Figura 146. Etapas da montagem do primeiro protótipo de cela de fluxo microfluídico para eletroquímica.

Mas a “máscara” interna de silicone ficou com uma superfície muito irregular como mostra a figura 147.
Figura 147. Superfície irregular da máscara de silicone do primeiro protótipo de cela de fluxo microfluídico para eletroquímica.

Substitui a “máscara” interna de silicone por uma máscara de borracha como mostram as figuras 148 e 149.
Figura 148. Etapas de montagem da cela de fluxo microfluídico para eletroquímica com recheio de borracha.

Figura 149. Etapas de montagem da cela de fluxo microfluídico para eletroquímica com recheio de borracha.

Tentei fazer um furo mais longo na lateral para ter mais estabilidade na fixação das mangueiras mas percebi que é difícil fazer um furo alinhado pois a perfuração sofre uma “inclinação” perfurando a face da placa de acrílico antes da posição desejada como mostra a figura 150.
Aproveitei as placas e montei uma cela de fluxo com o recheio de borracha para testar se haveria “vazamento” de água entre a borracha e a placa de acrílico. E logo no primeiro teste foi possível observar a entrada de água entre a manta de borracha e a placa de acrílico como mostra o destaque na figura 151.
Qual a diferença de capacitores cerâmicos, poliéster e eletrolíticos?
A Miniaturized FIA System for the Determination of Residual Chlorine in Environmental Water Samples
Simple Miniaturized Amperometric Flow Cell for Monitoring Residual Chlorine in Tap Water
Building an Arduino based potentiostat and Instrumentation for Cyclic Voltammetry
Design, Development, and Characterization of an Inexpensive Portable Cyclic Voltammeter
A LOW COST POTENTIOSTAT DEVICE FOR MONITORING AQUEOUS SOLUTION
Peter Kissinger, William R. Heineman-Laboratory techniques in electroanalytical chemistry-CRC Press (1996), página 181
Microcomputer-controlled cyclic voltammetry, Journal of Chemical Education, https://doi.org/10.1021/ed063p325